Формулы определения периметра, площади и сторон треугольника

Помещение неправильной формы

Итак, рассмотрим на конкретных примерах способы вычисления метража:

1. Кухня. Каждая кухня имеет вентиляционную шахту, радиатор вдоль окна, дверь, окно и встроенную полку для хранения. Посчитаем чистую площадь стен кухни для поклейки обоев.

Данные кухни:

Высота =2,5 м;

Ширина=3 м;

Длина =3,5м.

Размер двери: ширина =0,8 м, высота = 2,0 м;

Размер окна: ширина 1,2 м, высота = 1,5м;

Вентиляционная шахта имеет следующие габариты: ширина =50 см, длина =30 см; высота = 2,5 м;

Габариты радиатора: ширина = 10 см, длина = 100 см, высота = 50 см.

Вычислим чистую площадь:

Сначала находим общую площадь: (3,5 м*2)+(3 м*2)*2,5 м = 32,5 м2;

Окна: S чистая = 1,2 м*1,5 м = 1,8 м2;

Двери: S чистая = 0,8 м*2,0 м = 1,6 м2;

Вентиляционная шахта: S чистая = (50 см * 2) + (30 см *2) *2,5 м = 400 см2 или 0,40 м2;

Встроенная полка: S чистая = (20 см*2) + (50 см * 2) *2,5 м = 350 см2 или 0,35 м2;

Площадь поверхности радиатора: (10 см *2) + (100 см *2) * 0,5 м = 110 см2 или 0, 11 м2.

Теперь определяем количество чистых квадратных метров, путем вычитания их общей площади: S чистая стен кухни = 32,5 м2 — 1,8 м2- 1,6 м2- 0,40 м2- 0,35 м2 — 0,11 м2 = 28,24 м2.

Полезный совет: для подсчета количества трубок обоев, необходимо разделить чистую площадь на количество листов в трубке.

Стандартная трубка имеет следующие размеры: ширина = 50 см, длина полотна = 10 м. Высота стен квартиры составляет 2,5 м, и этого следует, что в одну трубку обоев входит 4 бумажных полотна: 10 м /2,5 м= 4 листа.

Подсчитаем, сколько же нужно трубок, чтобы поклеить кухню:

28,24 м2 /4 = 7,06 трубок. Но так как, бумажное полотно может содержать рисунок с шагом 0,3 или 0,5, то следует округлить количество трубок до 8.

1. Ванная комната. Рассчитаем количество ящиков плитки для стандартной ванны. Чтобы правильно посчитать квадратуру помещения, необходимо производить измерения с учетом подрезки керамической плитки.

Нам известен стандартный размер двери: ширина =0,8 м; высота = 2,0 м.

Размер типовой ванной комнаты составляет: ширина 2,3 м; длина = 1,6 м, высота= 2,5 м.

Вычисляем чистую площадь ванны:

S ванны = (2,3 м*2) + (1,6 м*2) *2,5 м = 19,5 м2.

Затем, вычитаем следующие значения:

S чистая = 19,5 м2 — 1,6 м2 = 17,9 м2.

Для того, чтобы подсчитать, сколько же ящиков плитки Вам необходимо, следует определиться с размером керамического изделия. Плитка бывает следующих размеров: 10х10; 10х20; 20х30; 30х30. Возьмем более распространенный вариант: 30х30.

В одной упаковке находится 10 штук и, зная размер плитки, можно высчитать количества штук на 1 м2:

Определим, количество целых плиток и количество подрезки:

17,9 м2 / 9= 1,9 — округляем и получаем 20 коробок целых плиток;

20 * 7 = 140 маленьких плиток, размером 10х10.

Если класть плитку по плоскости без подрезки, то следует брать 20 ящиков, а если с подрезкой, то 16.

1. Балкон. Чтобы получить чистую площадь балкона, необходимо измерить рамы с остеклением. Периметр балкона вымеряется без учета окон.
2. Гараж. Как правило, гараж представляет собой коробку с маленьким окном. Для подсчета чистой площади, необходимо измерить размеры ворот.

Померить площадь круглого окна, перекрытия, стены здания в виде неправильной формы или восьмигранника, можно с помощью подручных средств.

Возьмите рулетку и вымеряйте максимальный диаметр круга, например, он получился 100 см. Вычисляем радиус: 100 см /2 =50 см — это ¼ круга в виде треугольника.

Если круг зрительно разделить на 4 части, и соединить точки прямыми линиями, мы получим 2 равнобедренных треугольника или 1 квадрат. Нам известна часть равнобедренного треугольника, следовательно, все стороны будут по 50 см. Остается найти площадь квадрата, где все стороны по 50 см. Вычислить общую площадь любой конструкции можно с помощью онлайн — программы.

Смотрите видео, в котором мастер подробно разъясняет, как правильно высчитать площадь стен в квартире:

Как определить площадь комнаты в квадратных метрах

Прямоугольная комната

Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса.

К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м.

Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.

Понятие и классификация жилищных фондов. Юридическое значение.

Понятие жилищного фонда содержится в статье 19 ЖК РФ – под жилищным фондом принято понимать совокупность жилых помещений находящихся на территории РФ.

Особенности:

1. Характеризуется множественностью субъектов, то есть собственников отдельных частей этого фонда (граждане, юридические лица, публично-правовые образования).

2. Может переходить из одной формы собственности в другую форму.

Виды:

1. в зависимости от формы собственности

   1. частный. Это совокупность жилых помещений, которые находятся в собственности граждан и в собственности юридических лиц. Законодатель не ограничивает приобретение жилых помещений по количеству, размерам, стоимости. Юридические лица – это помещения построенные или приобретенные за счет собственности соответствующего юридического лица

   2. государственный. Это совокупность жилых помещений принадлежащих РФ и субъектам РФ. Поэтому как правило этот жилищный фонд делят на два уровня:

      1. жилищный фонд РФ (жилые помещения находящиеся в собственности РФ)

      2. жилищный фонд субъекта РФ (в собственности субъектов)

Сюда включается и помещения принадлежащие на праве хозяйственного ведения и оперативного управления. Права собственника осуществляют от имени собственника соответствующие органы (ОГВ)

1. 1. муниципальные. Это совокупность жилых помещений находящиеся в собственности муниципальных образований

2. В зависимости от цели использования:

   1. Жилищный фонд социального использования. Данные жилы помещения предоставляются по договору социального найма и участвуют здесь только государственные и муниципальные жилищные фонды

   2. Специализированный жилищный фонд. Это жилые помещения предназначенные для проживания отдельных категорий граждан, которые указаны в законе. Здесь также участвует только государственный и муниципальный жилищный фонд

   3. Индивидуальный жилищный фонд. Это помещения которые используются гражданами для своего проживания. Проживать могут быть собственники и члены их семей, а также иные граждане, но на безвозмездной основе. Индивидуальный жилищный фонд – это только частный жилищный фонд.

   4. Жилищный фонд коммерческого использования – это совокупность жилых помещений которые используются собственниками для проживания граждан на возмездных условиях или на условиях возмездного пользования.

Жилищный фонд подлежит государственному учету в порядке устанавливаемом правительством РФ. Государственный учет включает в себя в том числе проведение технического учета жилищного фонда. Технический учет включает в себя:

1. Техническую инвентаризацию

2. Техническая паспортизация

Значение классификации:

1. Помогает определить собственника жилого фонда, который несет ответственность за эксплуатацию и содержание соответствующего жилья. Этому же способствует государственный учет (постановление правительства о государственном учете жилищного фонда)

2. Осуществляется государственный контроль за использованием и сохранностью жилищного фонда

3. Определяется каким образом можно распоряжаться жилым помещением

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м². В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

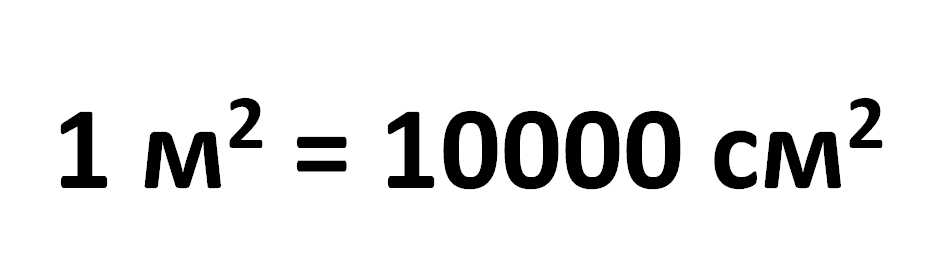Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Площадь фигур на клетчатой бумаге. Начальный уровень.

Алгоритм нахождения площади фигур на клетчатой бумаге:

Способ 1: (удобен для стандартных фигур: треугольника, трапеции и т.д.)

1. Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади.
2. Подставить найденные значения в уравнение площади.

Способ 2: (очень удобен для сложных фигур, но и для простых неплох)

1. Достроить искомую фигуру до прямоугольника.
2. Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника.
3. Из площадипрямоугольника вычесть сумму площадей всех лишних фигур.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Статья по теме: Самостоятельно облицовываем ступени лестницы плиткой, керамогранитом

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

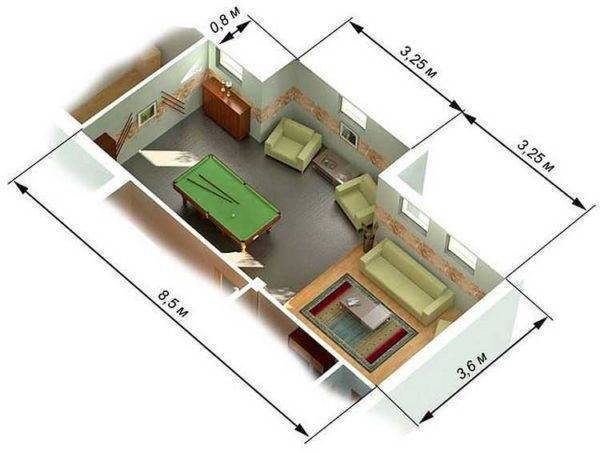
Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

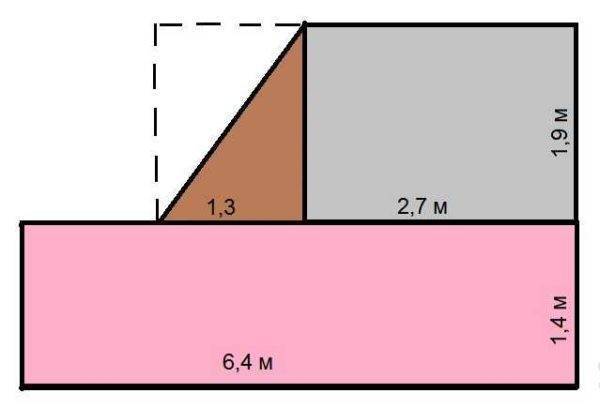
Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Статья по теме: Утепление пенополиуретаном своими руками: плюсы и минусы (фото, видео)

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

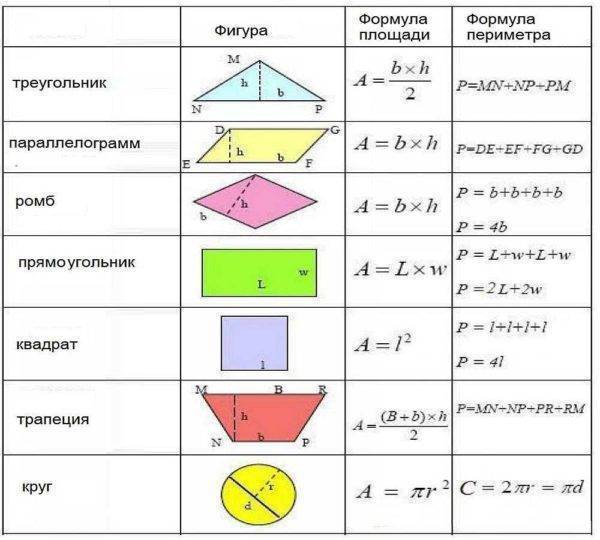
Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов

В результате получаем площадь пола

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как квадратные метры перевести в погонные и просто в метры?

Правильный ответ — Нет, потому что квадратные метры и линейные метры являются единицами измерения разных категорий. Квадратные метры измеряют площадь, а погонные метры измеряют только длину изделия.

Вот краткое изложение терминов: квадратный метр и погонный метр.

Квадратный метр (кв.м; м2) в Международной системе единиц (СИ) — это площадь квадрата со стороной, равной 1 метру. Квадратный метр — это мера площади стен, полов, недвижимости, где площадь, например, офиса или квартиры равна площади пола. Или, если вам нужно посчитать количество керамической плитки на стене или линолеума на полу, вам нужно умножить длину на высоту и получить площадь в квадратных метрах. Хотя сам линолеум продается погонными метрами, но об этом ниже.

Обозначения в квадратных метрах (m2) используются в …

• Обмер зданий, домов, квартир, комнат;
• Замер облицовочных и террасных материалов;
• Измерение настила крыш и полов;
• Измерение площади, занимаемой оборудованием, мебелью

Концепция квадратных метров

Перевести квадратные метры в погонные метры, а просто в метры — НЕТ!

Один метр (рулон ткани, изделие, забор, мебель) — это длина вне зависимости от ширины. Так как цена материала входит в стоимость 1 погонного метра вагонки, линолеума или куба. Погонный метр линолеума шириной 3 метра будет, конечно, дороже линолеума шириной 2,5 метра.

Иногда погонные метры используются и при изготовлении кухонной мебели для удобных расчетов. Например, производитель подсчитал, что кухонный шкаф длиной 3 метра и шириной 60 сантиметров с необходимым количеством полок, ящиков, дверок будет стоить 1200 долларов по курсу Нацбанка. А как известно, кухня в наших квартирах разная, в основном небольшая, поэтому производитель ставит цену за 1 погонный метр в 400 долларов. Клиент может уместить только 2,5 метра. Обсуждаем стандартное оборудование, размещение полок, ящиков и вывозим цену 1000 долларов.

Подробнее: Как сделать высокие грядки своими руками

400 долларов США x 2,5 млн = 1000 долларов США

Обозначения в погонных метрах используются для измерения:

• Полы в рулонах (ткань в рулонах, ковролин, линолеум …);
• Доски, рейки, блок-хаус, плинтусы, иногда трубы, фитинги;
• Стоимость от цены мебели (кухни) со стандартной техникой и фурнитурой.

Примеры решения задач

Выведенные формулы можно с легкостью применять для решения разнообразных задач по геометрии. Для понимания, как их следует использовать, следует рассмотреть несколько примеров.

Описанная и вписанная окружности

Дан некоторый равноугольный треугольник. Известно, что разница между радиусами описанной и вписанной окружностей составляет 3 см. Следует найти площадь фигуры.

На первый взгляд может показаться, что нахождение решения этой задачи требует проведения некоторых промежуточных вычислений, но это не так. Если вспомнить, что радиус описанной окружности R ровно в 2 раза больше величины r, то их разница является не чем иным, как самим радиусом вписанной окружности r. Для получения ответа на задачу следует всего-навсего воспользоваться известной формулой и вычислить S:

S = 3*30,5 *r 2 = 46,765 см 2 .

Тетраэдр и его поверхность

Тетраэдр является объемной фигурой, которая ограничена четырьмя гранями, являющимися равноугольными треугольниками. Необходимо определить площадь поверхности этой геометрической фигуры, если известно, что ее объем составляет 100 см 3 .

Чтобы посчитать необходимую площадь, следует найти эту величину всего лишь для одного равностороннего треугольника, а затем полученное число умножить на 4. Из курса стереометрии известно, что объем тетраэдра рассчитывается по следующей формуле:

V = 20,5 /12*a 3 .

Отсюда можно получить длину стороны a:

a = (12*V/20,5)^(1/3).

Теперь можно применить формулу для расчета площади S через a:

S = 30,5/4*a 2 = 38,81 см 2 .

Получилась площадь одной грани тетраэдра. Поскольку объемная фигура состоит из четырех одинаковых треугольников, то площадь его поверхности St составит:

St = 4*S = 155,24 см 2 .

Таким образом, высокая симметрия равностороннего треугольника позволяет рассчитывать его площадь, зная всего один линейный параметр фигуры. Чаще всего таковым является высота, сторона основания или радиусы вписанной и описанной окружностей.

Предыдущая

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.