Катеты прямоугольного треугольника

Виды конструкционного решения крыш

Существует 4 вида конструкционного решения крыши, поэтому в зависимости от уклона кровли, она может быть:

• плоской. В действительности абсолютно плоских перекрытий зданий не строят, поскольку на них постоянно будет задерживаться влага от дождя или растаявшего снега. Уклон крыши не может быть меньше 3-х градусов (подробнее: «Виды кровли для крыши — классификация «);
• скатной;
• пологой;
• высокой.

Поскольку величину уклона измеряют как в процентах, так и в градусах, имеется специальная таблица, согласно которой можно определить соотношение между данными величинами. Например: угол наклона ската равен 30 градусов, тогда уклон кровли в процентах составит 57,7%.

Климат местности

Угол наклона кровли также зависит от климатических условий, в которых сооружено здание. Почему? В местности, где крыши дома в большинстве случаев имеют минимальный угол наклона, часто дуют сильные ветра. Таким образом, конструкция уменьшает неблагоприятное воздействие ветра на крышу в целом. Кровли, которые имеют меньше 10 градусов уклона, практически не подвержены такому влиянию. Но здесь возникает вероятность срыва ветряным потоком кровельного материала.

Как посчитать оптимальный вариант? Специалисты рекомендуют возводить кровли в 35 градусов в местностях с небольшими ветряными нагрузками. При сильном ветре крыша должна быть 15-25 градусов.

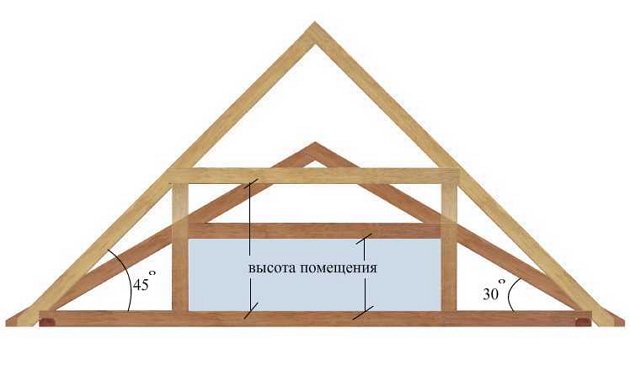
Какой должен быть угол для мансард? Для его расчета необходимо длину торца разделить вдвое. А высота ската в торце стандартна (1,8 м).

В местностях, где часто выпадают большие осадки, угол наклона может быть равен 60 градусам.

Минимальный уклон кровли из профлиста

Одной из наиважнейших задач при строительстве кровли из профлиста является выбор правильного уклона. Не все знают, что уклон кровли играет основную роль в ее прочности и степени защиты от атмосферных осадков. Небольшой уклон может пагубно отразится на ее прочности и степени защиты, а слишком большой – на ее ветроустойчивости, а правильно подобрать наклон крыши, не нарушив эстетику и дизайн дома, бывает не просто.

Минимальный уклон кровли зависит от:

• кровельного материала
• прочности стропильной системы
• климатических условий района

Минимальный и оптимальный уклон кровли из профлиста

В таблице указаны минимальный и оптимальный градус наклона для крыши, накрытой профлистом.

Необходимо знать, что при уклоне кровли менее 12 градусов, необходимо проводить герметизацию горизонтальных швов, для того, чтобы предотвратить попадание атмосферных осадков на стыках профлистов.

В следующей таблице указан горизонтальный нахлест при различных углах уклона кровли из профлиста:

Кроме расчета угла кровли, иногда уклон рассчитывают в относительных величинах, далее мы рассчитаем на реальных примерах обе величины.

Как рассчитать уклон кровли по схеме в градусах

Давайте на примере обычной двухскатной крыши рассчитаем угол уклона. На схеме видно, что А – это угол уклона левого ската, а В – второго. Для того, чтобы их рассчитать, нам необходимо знать высоту кровли h и длину горизонтальной проекции скатов с и d.

Если кровля симметрична, то длины с и d будут равны и чтобы их найти, нам необходимо будет длину стены разделить пополам.

Пример расчета угла уклона кровли с помощью схемы

Из моей схемы видно, что кровля у нас симметричная, т.е. углы А и В будут одинаковы. Давайте теперь попробуем рассчитать углы на реальном примере.

Допустим, у нас есть следующие значения:

• Длина стены = 12м
• Высота кровли h = 3м

Теперь необходимо рассчитать с и d. В нашем случае с = d = 12/2 = 6м, то есть с и d у нас по 6 метров.

На схеме мы видим прямоугольный треугольник, и чтобы найти его угол А, необходимо рассчитать тангенс этого угла. Из геометрии помним, что тангенс угла равен отношению противолежащего катета к прилежащему. Противолежащим катетом является высота кровли (h), а прилежащим катетом является (с).

В нашем случае, тангенс угла равен 3/6 = 1/2 или 0,5.

С помощью инженерного калькулятора или таблицы тангенсов вычисляем угол, который в нашем случае будет равен примерно 27 градусов.

Уклон кровли в относительных величинах

Иногда уклон кровли измеряют не в градусах, а в относительных величинах. В этом случае достаточно разделить высоту кровли (h) на горизонтальную проекцию ската (с).

Если взять предыдущий пример, то у нас получится, что уклон равен 1/2. Ну а если необходимо в выразить уклон в процентах, то 0,5 нужно умножить на 100%, и получится 50%.

Достоинства и недостатки различных уклонов кровли из профлиста

При небольшом уклоне, так же как и при большом, у кровли из профлиста будут проявляться свои достоинства и недостатки.

Маленький уклон кровли (12-20градусов)

Достоинства такой кровли:

• ветроустойчивость
• простота монтажа
• небольшой расход материала

Недостатки кровли с маленьким уклоном из профлиста:

• возможность попадания осадков в стыковочных местах
• зимой большая нагрузка от снега
• возможно, придется зимой чистить крышу вручную
• проблематичный мансардный этаж

Большой уклон кровли из профлиста ( >45 градусов)

Достоинства кровли с большим уклоном:

• исключено попадание осадков в стыки профлиста
• увеличенное чердачное пространство
• зимой снег залеживаться на профлисте практически не будет

Недостатки большого уклона кровли:

• неудобство монтажа профлиста
• огромная парусность такой крыши
• постоянное скатывание снега с кровли из профнастила

Минимальный уклон кровли из профлиста Минимальный уклон кровли из профлиста, читайте и подписывайтесь на Stroitelstvo.Guru!

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.

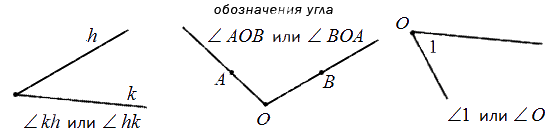
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

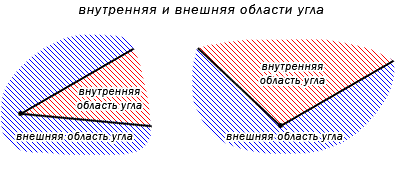
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Внутренняя область угла – элемент, служащий для второго определения угла.

Определение 5

Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.

Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.

Пример расчета уклона кровли в градусах

Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.

Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.

Итак, процесс изготовления:

1. Вбиваем в длинную доску два гвоздя на расстоянии L= 5 метров друг от друга. Это расстояние нужно выполнить точно, Разметку лучше делать рулеткой.
2. Надеваем на гвозди два кольца, например от ключей, и туго стягиваем кольца прочным шпагатом или веревкой. Веревку или шпагат надо надежно закрепить на кольцах.
3. Вбиваем в доску два гвоздя на расстоянии L=4 метра и повторяем операцию по пункту 2.
4. Повторяем то же самое при L=3. Все. Угольник готов.

Проверим перпендикулярность вертикального бруса к горизонтальной платформе. Закрепим с помощью гвоздей один из тросиков, например трехметровый, на вертикальном брусе в точках 1 и 2. На те же гвозди оденем кольца пяти и четырехметровых тросиков, сводим свободные концы вместе и натягиваем конструкцию. Если точка 3 совпала с горизонтальной платформой – все в порядке. Угол 90 градусов.

Разумеется, что можно делать угольник не из трех отдельных тросиков, а из одного, выполненного треугольником. Тогда потребуется только три кольца, правильно расположенных на веревке.

Похожий вариант проверки рамы приведен на фото. А вот еще вариант проверки той же рамы, если у вас нет угольника, но есть металлический метр.

Отмерьте от угла рамы два катета по 60 и 80 сантиметров, приложите к рискам линейку. Если катеты измерены точно и метр линейки совпал с рисками, то рама сделана, верно. Угол прямой.

И, наконец, правильно поставим забор на приусадебном участке.

Натяните вдоль забора один из катетов нашего угольника и закрепите его колышками. Растяните наш угольник и забейте третий колышек. Вы получили прямой угол. Можно ставить забор.

Все эти фокусы с веревочным угольником основаны на школьной формуле: « квадрат гипотенузы равен сумме квадратов катетов».

Целые числа три четыре и пять, удовлетворяющие этому условию, легко запоминаются. Эти числа можно кратно изменять.

Можно, например, сделать отрезки длиной 1,5 2 2,5 метров, или 0,6 0,8 1 метр и даже 0,3 0,4 0,5 метра. Нужно только учесть, что чем меньше размер отрезков, тем точнее нужно выполнить их длину.

Source: metinvest-ekb.ru

Расчет двускатной крыши

Представляем бесплатный калькулятор по расчеты двускатной крыши. Онлайн расчет обрешетки, угла наклона стропил и необходимого количества материалов.

Дополнительная информация о калькуляторе

Онлайн-калькулятор двускатной (двухскатной) крыши поможет вам рассчитать угол ската, размер и количество стропил, количество обрешётки, а также объём нужных материалов в режиме онлайн. В расчётную базу заранее внесены такие распространённые кровельные материалы, как металлочерепица, шифер, ондулин, черепица из керамики, битума, цемента и другие материалы.

Двускатная крыша (также встречаются написания «двухскатная крыша», «щипцовая крыша») — вариант крыши с двумя скатами, идущими от конька до наружных стен здания. На сегодня это самый распространённый вид крыш, благодаря простоте исполнения, невысокой себестоимости и привлекательному внешнему виду.

Стропила в конструкции такой крыши попарно опираются друг на друга и соединяются обрешёткой. Торцевые стороны сооружения с такой крышей имеют форму треугольника и называются фронтонами (иногда – щипцами). Обычно под двускатной крышей устраивается чердак, а на фронтонах для освещения проделываются небольшие чердачные окна.

Заполняя поля калькулятора, обратите внимание на значок «Дополнительная информация» , под которым скрываются пояснения по каждому пункту. Результаты расчетов также сопровождаются пояснениями, с которыми вы можете ознакомиться ниже. Результаты расчетов также сопровождаются пояснениями, с которыми вы можете ознакомиться ниже

Результаты расчетов также сопровождаются пояснениями, с которыми вы можете ознакомиться ниже.

Также вы можете задать свой вопрос или поделиться идеями по улучшению этого калькулятора. Будем рады вашим отзывам!

Пояснения к результатам расчетов

Угол наклона крыши

Так называется угол, под которым скат и стропила наклонены к плоскости потолка. Расчеты выполнены с учетом того, что планируется строительство симметричной двускатной крыши. Вводя угол, вы можете не только рассчитать нужное количество материалов для данного угла, но и проверить, возможно ли построение крыши под этим углом из выбранных вами материалов. Уменьшить или увеличить угол можно, изменив ширину основания или высоту подъёма: эти параметры жёстко взаимосвязаны.

Площадь поверхности крыши

Суммарная площадь скатов крыши, включающая площадь свесов заданной длины. Определяет количество кровельного и подкровельного материала, требуемого при строительстве крыши.

Примерный вес кровельного материала

Предположительный суммарный вес кровельного материала.

Количество рулонов изоляционного материала

Требуемое количество подкровельного материала, с учётом необходимого нахлёста в 10%. В расчётах мы исходим из рулонов длиной 15 метров и шириной 1 метр.

Нагрузка на стропильную систему

Максимально возможная нагрузка с учетом ветровых и снеговых нагрузок, приходящаяся на стропила.

Длина стропил

Стропила измеряются от основания ската до конька крыши.

Количество стропил

Суммарное количество стропил, необходимых для стропильной системы крыши при заданном шаге.

Минимальное сечение стропил

Чтобы обеспечить крыше достаточную прочность, необходимо выбрать стропила с предложенными здесь вариантами сечений.

Количество рядов обрешётки

При заданных вами параметрах потребуется данное количество рядов обрешетки. Если вам нужно определить количество рядов для одного ската, то данное значение нужно разделить на 2.

Равномерное расстояние между досками обрешетки

Чтобы исключить перерасход материалов и избавить себя от лишней работы по подрезке, вам нужно выбрать данное расстояние между досками обрешётки.

Объем досок обрешетки

Количество досок требуемых для обрешетки всей крыши (в кубических метрах).

Примерный вес досок обрешетки

Общий вес досок, используемых при обрешетке.

Расчет двускатной крыши Бесплатный калькулятор по расчеты двускатной крыши. Онлайн расчет обрешетки, угла наклона стропил и необходимого количества материалов.

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами

Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х2. Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с2– это площадь большого (на рисунке – синего)квадрата, а х2 – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

10:2 = 5

Другой катет находим с помощью теоремы Пифагора:

Градусы электрические: отклонение между напряжением и током

Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.

Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом – все светится, крутится, работает.

Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.

Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.

Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!

Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения – косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.

Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.

И не говорите теперь, что косинус – это абстракция, которую мы оставили в школе навсегда…

Разуклонка кровли

Разуклонка – это ряд мероприятий, применяемых для создания наклона на плоских крышах, устройства на них коньков и ендов. Благодаря этому уклон односкатной крыши способствует решению проблем с накоплением осадков на ее поверхности. Уклон нужно просчитать заранее. ещё до того, как сделать односкатную крышу. Минимально допустимым показателем для плоских кровель считается величина 1,5 градуса (подробнее: «Какой минимальный уклон плоской кровли «). Наклон ската необходимо обустроить таким образом, чтобы вода с его поверхности стекала в водоприемные воронки. Для этих целей применяют керамзит или цементные стяжки, но последние значительно увеличивают нагрузку на кровлю.

Если разуклонку выполняют при проведении ремонта, а не при строительстве нового здания, тогда используют плитные материалы, а также пенополиуретан или пенобетон.

Какую кровлю выбрать, подробнее на видео:

Как измерить угол между стен. Несколько способов.

Какой угол образуют стены. Первый способ – измерение.

Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.

Для чего это нужно делать? – чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.

К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.

Собственно, когда причины выяснили и необходимость измерения угла очевидна – дело за малым – измерить угол. Если у Вас имеется в домашнем арсенале угломер – тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.

Первое что необходимо сделать – это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:

• От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм. и ставите точки.
• Далее измеряете диагональ – т.е. расстояние между точками.

Итак например у нас есть три размера – катет 500мм., 500мм. и диагональ 700мм.

Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.

1. Чертим горизонтально отрезок 500мм. с точками “АБ”. (см. чертеж ниже.)
2. Чертим окружность с радиусом 500мм. с центром в точке “В”.
3. Чертим вторую окружность с радиусом 700мм. с центром в точке “А”.
4. В точке пересечения окружностей ставим точку “С”.
5. Соединяем точки “В” и “С” отрезком и получаем наш угол.
6. Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.

Когда чертеж построен, мы можем в заключении сделать вывод – измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т.к. 1 градус величина довольно малая.

Какой угол образуют стены. Второй способ – расчёт.

1. От угла отмеряем 1000 мм (чем больше, тем лучше – погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками),
2. Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + b 2 – c 2 ) / (2 • a • b)

Получив cos(γ) угла, далее через функцию arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (1000 2 + 1000 2 – 1500 2 ) / (2 • 1000 • 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.

Теги: #Как высчитать градусы угла

Как сделать угол прямым

Стены выравниваются по очереди

Все зависит от величины уклонов стен. К незначительным относятся отклонения не более 20 мм. При проведении работ следует придерживаться некоторых правил:

1. Выставление вертикальных маяков является обязательным.
2. Соблюдение последовательности при нанесении раствора: сначала делается наброска жидким раствором, а после его схватывания производится окончательное выравнивание поверхности стены.
3. Нанесение толстого слоя раствора не рекомендуется, так как смесь под собственным весом отвалится, не успев схватиться.
4. Первоначально выравнивается правилом по маякам одна стена, затем — вторая.
5. При наличии правила в виде большого металлического угольника выравнивание происходит движением инструмента вверх-вниз по маякам. Излишек раствора срезается, а в недостающих местах — набрасывается.

При больших перепадах и отклонениях используйте армирующую сетку

При отклонении свыше 2 см потребуется проведение дополнительных операций:

• армирование путем установки ;
• путем оплетения проволоки по предварительно забитым дюбелям, гвоздям или шурупам. Зависит от стенового материала: бетон, кирпич, ракушняк, пенобетон, пеноблок;
• набивка дранки в деревянных домах.

Если стены имеют небольшое отклонение, то выравнивание производится непосредственно между ними, а также между стеной и потолком. При этом раствор наносится в углы и выравнивается угловым правилом. Дальше от угловой линии раствор на стене сводится на нет. Подробнеее о смотрите в этом видео: