Формула площади
Содержание:
- Общие сведения
- Как посчитать площадь комнаты: методика расчета по полу
- Расчет площади помещения со стандартной формой
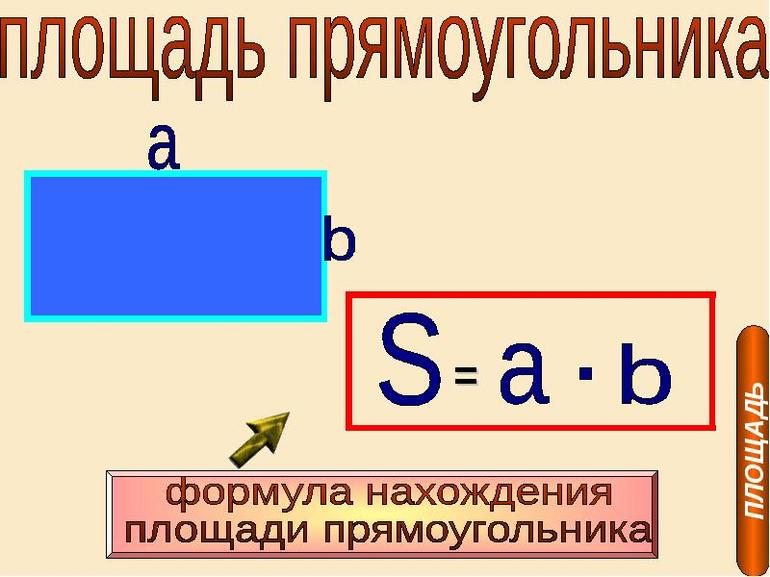
- Информация о прямоугольнике
- Площадь фигуры
- Измеряем площадь сложных фигур
- Поверхность тела и ее площадь
- Определение понятия
- Как рассчитать площадь комнаты – пошаговая инструкция
- Определяем площадь пола разной геометрии
- Пол оригинальной формы
- Параллелограмм и ромб
- Советы и рекомендации
- С чего начинать
Общие сведения
В различных задачах с физико-математическим уклоном приходится вычислять площадь прямоугольника. Однако формула расчета применяется не только в математике и физике, но и во время ремонтных работ. Например, следует посчитать количество расходных материалов, которое зависит от квадратуры комнаты или здания.

Очень важно не только знать основные соотношения, но и корректно переводить единицы измерения из одной в другую. От знаний полностью зависит экономия денежных средств
Например, при клейке обоев в комнате требуется определенное количество рулонов. Это количество можно купить в строительном магазине «на глаз» или рассчитать квадратуру комнаты. Во втором случае можно существенно сэкономить. Для того чтобы посчитать квадратные метры помещения, нужно вычислить его площадь.
Площадь фигуры
Площадью двумерной фигуры является численная характеристика, которая показывает ее размерность. Она обозначается литерой S и измеряется в квадратных единицах (мм 2, см 2, дм 2и т. д.). Не каждый элемент геометрии имеет площадь. Прямая, луч, отрезок, точка не имеют двумерной размерности. Фигуры, у которых она присутствует, являются квадратируемыми. Если значения их S равны, то они являются равновеликими.
Для вычисления значения двухплоскостной размерности фигуры применяется интегральный метод. Однако бывают частные случаи, когда вычислять интеграл необязательно. Существуют определенные формулы, полученные с помощью интегрального метода. Чтобы ими воспользоваться, нужно просто подставить числовые значения сторон.
Единицы измерения

При решении задач на нахождение значения площади нужно знать единицы ее измерения. Кроме того, следует правильно выполнять перевод одной единицы в другую. В системе исчисления используются квадратичные единицы измерения. За основу следует брать размер стороны прямоугольника. Например, при указании площади в кв. м нужно измерять в метраже стороны объекта. Это стандартная единица измерения площади.
Существуют также производные единицы. Самой маленькой из них является квадратный миллиметр (кв. мм или мм 2). В некоторой литературе или программировании можно встретить такую запись: sqr (m), которая означает квадратный метр. Основные производные единицы площади:
-
1 см 2 = 100 мм 2.
-
1 дм 2 = 100 см 2.
-
1 м 2 = 100 дм 2 = 10000 см 2.
-
1 км 2 = 1000000 м 2.
-
1 ар (а) = 1 сотка = 100 м 2.
-
1 гектар (га) = 10000 м 2.
Последние применяются для измерения земельного участка. Однако необязательно их все помнить. Они легко выводятся при помощи простейших математических вычислений. Например, для выполнения расчетов нужно перевести кв. м в кв. см. Однако человек мог забыть, сколько см 2в квадратном метре. Следует взять метрическую форму (1 м = 100 см). Затем нужно возвести обе части выражения в квадрат: 1 м 2 = 100 * 100 = 10000 (см 2).
Как посчитать площадь комнаты: методика расчета по полу
Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны
В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации
В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.

В таблице можно посмотреть соответствие площади на полу с показателями для стен при определенной высоте потолка
Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда требуется учитывать разные углубления и выступы в стенах.
При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью
Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.
Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.

Полы сложной конфигурации требуют особой внимательности и использования специальных формул
Измерения
Перед тем как измерить комнату в квадратных метрах, необходим минимальный набор предметов:
- калькулятор;
- рулетка;
- карандаш;
- лист бумаги.
На бумаге необходимо сделать подробный план помещения. Каждая стена должна быть измерена с использованием рулетки.
Вторым этапом является проставление полученных измерений на плане. Лучше всего сразу делать это в метрах, но точность каждого замера должна быть до 1 сантиметра. Это необходимо для того, чтобы при выборе необходимого количества материалов, удалось максимально точно подобрать метраж требуемого материала. Рулонные напольные покрытия продаются в погонных метрах.

Округлять можно только в случае небольшого увеличения, чтобы в случае непредвиденных обстоятельство, было достаточное количество материала.
Как высчитать квадратуру комнаты
Чтобы понять, как узнать общую площадь комнаты, необходимо воспользоваться простой формулой и перемножить показания длины на ширину. Как показано на рисунке длинная стена имеет длину в 7 метров а противоположная только 4. Выходит площадь пола будет равна 28 м2. Именно таким образом и находят квадратуру. Обязательно требуется помнить о небольшом запасе, который потребуется для подгонки и подрезки, причем чем сложнее будет вариант укладки, тем больше потребуется брать запас.
Расчет площади помещения со стандартной формой
Сегодня всё чаще можно встретить комнаты с непривычной конфигурацией: треугольные, круглые или трапециобразные.
Расчёт треугольной формы
Бывают помещения по виду напоминающие треугольник. Рассчитать площадь такой комнаты в квадратных метрах доступно как на калькуляторе, так и с использованием формулы.
- а — основание;
- h — перпендикулярная высота.

Чтобы провести расчёт, измеряется длина основания треугольника и высота, проведённая перпендикулярно основанию из противоположно расположенного угла. Единственное — проведение перпендикулярной при замере сделать не просто, особенно если не использовать специальный инструмент. Поэтому, полученные данные могут быть не точными.
Для расчёта S треугольника лучше воспользоваться формулой Герона. Она более сложная, но результат получается точнее.
- a, b,с — длины сторон;
- p — половина периметра (р = ½ (а + b + с)).
Так же, посчитать площадь треугольной фигуры можно на онлайн-калькуляторе.
Трапеция
Помещение, являющееся угловым, нередко имеет трапециобразную форму. Главная черта трапеции — расположение двух сторон в параллельной плоскости, а двух других — нет, они находятся под разными углами.
Для определения S трапециобразной комнаты делается замер двух параллельных сторон, и высоты — перпендикулярной линии между сторонами. Чтобы убедиться, что стороны расположены точно параллельно, нужно измерить высоту в нескольких местах.
Эти данные следует вставить в разделы калькулятора, или в формулу:
- A и B — длина сторон лежащих параллельно;
- h — высота.

Сделать данные вычисления потребуется, если определяется размер многоугольной комнаты. Допустим, имеется 5 углов, тогда многоугольник следует разделить на две фигуры — прямоугольник и трапецию, и сделать два расчёта, а результаты сложить.
Есть еще один способ, как рассчитать площадь трапециобразной комнаты в м2 — поделить трапецию на прямоугольные и треугольные фигуры, и определить размер каждой, а затем всё сложить.
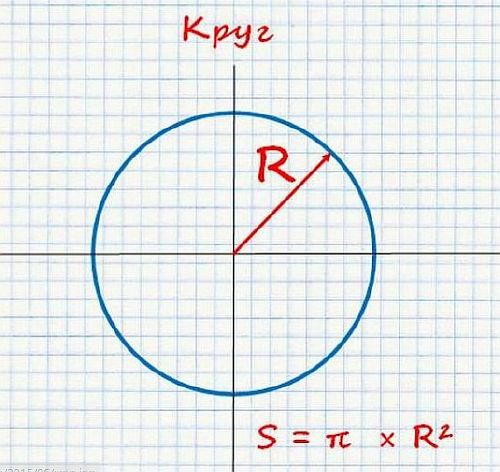
Круг
В новостройках встречаются участки здания с округлой формой (полукруг или четверть). Нередко это бывает при совмещённом балконе или эркере.
Сначала нужно определить значение выпуклой части, которое потом приплюсовывается к остальным результатам. Замеры округлых участков можно производить, используя гибкую рулетку или бечёвку.
Рассчитать S круга легко по формуле:
- n — коэффициент равный 3,14;
- R² — радиус круга в квадрате.
Сложнее подсчитать S отдельной части круга отсечённого хордой. Такие расчёты производятся по формуле:
Для таких вычислений подойдёт калькулятор, в нём есть специальная форма для расчёта площади круга.
Информация о прямоугольнике
Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.
Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.
Свойства и признаки
Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:
- Условие параллельности и равенства противоположных сторон.
- Наличие четырех прямых углов.
- Равенство диагоналей.
- Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
- Все стороны не равны между собой.
Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают
Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:
- Углы равны между собой 90 градусов.
- Противолежащие параллельные стороны равны.
- Сумма всех внутренних углов составляет 360.
- Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
- Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
- Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
- Точка пересечения диагоналей — центр симметрии.
- Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.
Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).
Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.
Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.
Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²

Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Измеряем площадь сложных фигур
Круг и треугольник — сложные формы для самостоятельного расчета. Как измерить квадратные метры круга, если у вас нет математического или инженерного образования? Опять же, применив формулу.
Как измерить размер окружности
Есть формула для вычисления площади круга. Существует постоянное число, отношение длины окружности к ее диаметру. Это число одинаково для всех размеров круга. Он называется пи и равен 3,14. Это число, которое используется в расчетах.
Шаг №1. Измеряем диаметр (это линия, проходящая через центр круга от одного края круга до другого). Пусть диаметр будет 3 м. Затем находим радиус — это половина длины диаметра. Это 1,5 м. Пишем радиус на листе бумаги.
Этап 2. Расчеты производятся по формуле S = RR2, где S — площадь круга, P — фиксированное число, R — радиус круга. Получается 3,14 х (1,5 х 1,5) = 7,065. Площадь этого района составляет 7 065 квадратных метров.
Но это площадь всего круга. Арка над дверью — полукруг. Таким образом, вам все равно придется разделить это число на два, а затем добавить его к прямоугольной области двери. 7.065. 2 = 3,53 м2.
Как измерить площадь треугольника
Если предыдущий хозяин квартиры был математиком, то, возможно, он сделал на потолке треугольные формы, которые нужно восстановить и подчеркнуть другим цветом или штукатуркой. Придется рассчитывать, чтобы не переплачивать.
Вычисление квадрата метра в треугольной фигуре начинается с пристального взгляда на фигуру.
Вам нужно найти основание треугольника, то есть линию, на которой опираются два других (как крыша на домике). Затем проведите линию от противоположной вершины до основания. Запишите эти два числа.
Шаг 1. Основание этого треугольника разделите на 2 и запишите. Этот выпуск нам пригодится в ближайшее время. Измерьте высоту и запишите ее.
Шаг 2. Вычислите площадь этого рисунка. Для этого используйте формулу: S = 0,5ah, где S — площадь треугольника, а — основание, а h — высота. Пример: основание составляет 3 м, а высота — 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Площадь треугольника 3,75 м2. Запишите их, чтобы не забыть о них.
Поверхность тела и ее площадь
Это мера того, сколько пространства находится внутри плоской формы. В общем случае площадь поверхности представляет собой сумму всех областей геометрических фигур, покрывающих поверхность объекта. Рассчитать площадь поверхности тела часто требуется в повседневной жизни, например, чтобы узнать сколько краски нужно купить, чтобы покрыть стену, или шифера для ремонта крыши дома.
Люди издавна научились определять площадь плоских геометрических фигур, используя метод сетки. Он заключается в том, что на измеряемую фигуру накладывают масштабированную сетку из простейших квадратов, например, 1х1 см. После чего можно легко рассчитать квадратную площадь, посчитав количество квадратов сетки внутри формы. В этом случае каждый квадрат сетки имеет ширину 1 см и высоту 1 см, и площадь этого квадрата сетки составляет один квадратный сантиметр.
Использование сетки для подсчета квадратов в форме — это очень простой способ определения площади, но он не может быть применен для определения площади сложных фигур. Площадь таких сложных объектов может быть рассчитана с использованием простых математических формул. Самые простые и наиболее часто используемые в жизни вычисления — это площади квадратов и прямоугольников, и надо знать, как рассчитать площадь в метрах.
Часто в реальности расчеты могут быть более сложными. Например, типичный план этажа комнаты может не состоять из простого прямоугольника или квадрата. В этом случае перед тем, как рассчитать общую площадь, нужно разделить измеряемую сложную поверхность на несколько простейших геометрических фигур.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Как рассчитать площадь комнаты – пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты
Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.
Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:
- рулетка;
- карандаш;
- бумага для записей;
- калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
- трезвость ума и ясность мыслей.
Пол
Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.
После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.
Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.
С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.
Если помещение неправильной формы
Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

- для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
- для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
- для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).
Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.
И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.
С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают стены.
Стены
Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой
А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.
Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.
Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.
Существует также ряд общих рекомендаций по проведению замеров.
Определяем площадь пола разной геометрии
Единицей измерения площади является метр квадратный. Площадь комнаты грубо определяется количеством квадратных метров, которые можно уложить на ее пол. Однако геометрия пола помещения не всегда бывает правильной квадратной или прямоугольной форму, а потому квадратные метры в каждом конкретном случае высчитываются в применение различных формул.
Как правильно посчитать площадь пола помещений разной геометрии:
- Комната, имеющая правильную геометрию, в которой нет ниш, колон и прочих выступающих или врезных элементов интерьера. В данном случае нужно измерить длину и ширину прямоугольника или квадрата. Посчитать квадратные метры можно по формуле:S = H*B, где S – искомая площадь, единица измерения метр квадратный;H – длина помещения, м;B – его ширина;В случае с квадратной комнатой достаточно длину ее стороны возвести в квадрат, так как длина каждой стены в этом случае будет одинаковой.
- Комната имеет сложную геометрию. Любую сложную фигуру в таком случае разбивают на несколько простых. Далее нужно измерить площадь пола (единица измерений – метр квадратный) каждой части помещения в отдельности и полученные результаты суммировать.
Если помещение имеет нишу. В таком случае комната делится на простые фигуры. Это прямоугольник основной части помещения и прямоугольник ниши. Площадь пола в каждом случае определяются отдельно, а затем суммируются.
Если комната имеет выступающие части. Определяют длину и ширину помещения (единица измерения — метры) без учета выступающих частей. Вычисляют общую площадь комнаты без учета площади колонн. Отдельно снимают замеры с выступающих частей и определяют их площадь. С первого результата отнимают площадь всех последующих площадей выступающих частей.
Если форма пола имеет вид трапеции. В таком случае пол в комнате условно разбивают на два треугольника и один прямоугольник. Общие квадратные метры пола в помещении вычисляют как общую сумму площадей полученных фигур. А можно воспользоваться формулой для вычисления площади трапеции. Допустим, что две параллельные стороны комнаты – это основания трапеции. Непараллельные стены – стороны трапеции. Из угла между меньшим основанием трапеции и ее стороной на большее основание опускает линию под прямым углом. Это будет высота трапеции. Узнает ее длину (метры). Также определяем длину непараллельных сторон комнаты.
Далее вычисления проводят по формуле:
- S – площадь искомой фигуры (метры квадратные);
- a – длина большего основания, метр;
- b – длина меньшего основания, метр;
- h – длина высоты трапеции, метр.
Если комната имеет одну полукруглую сторону. В таком случае условно делят помещения на прямоугольники, отделяя ту часть комнаты, которая имеет криволинейную сторону или сегмент. Далее определяют радиус полученной окружности. Это делают по формуле:
Если сегмент приравнивается половине окружности, то полученную площадь, делим на 2, если в комнате присутствует только четверть круга, по полученную площадь, делим на 4.
Ремонт линолеума своими руками
Главная » Разное » Как посчитать квадратуру комнаты, стен, потолка, пола
Пол оригинальной формы
Первое, что следует сделать при подсчёте площади пола неправильной формы — мысленно или на бумаге расчленить его на простые фигуры. После чего высчитать отдельно площадь каждой из них и суммировать результаты.

По ходу выполнения этого задания вы обязательно заметите, что фигуры сами по себе простые, а вот процесс вычисления их площади не всегда. Для каждой отдельной части придётся применять свою формулу в зависимости от её геометрии. Некоторые из них мы сейчас рассмотрим.
Треугольники
Проще всего иметь дело с прямоугольными представителями этого семейства. Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).
Если треугольник не имеет прямых углов, необходимо провести следующие действия:
- принять одну из его сторон за основание;
- провести от вершины к нему высоту;
- умножить одно на другое;
- результат разделить на 2.
В итоге формула будет иметь такой вид: S=a*h/2. Где a и h — длина основания и высота соответственно.

Для любителей экзотики существуют и другие варианты. Например, формула Герона, или подсчёт с помощью радиуса вписанной в треугольник окружности. Но проще всё-таки будет считать через основание и высоту.
Круги и овалы
Такие геометрические формы в строительстве встречаются редко, но всё же встречаются. Чтобы рассчитать площадь круга достаточно найти его радиус и подставить в уравнение: S=πr2. Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.

Площадь овала (эллипса) вычисляется похожим образом. Только вместо радиуса необходимо найти длину двух его полуосей — длинной (a) и короткой (b). Дальше — по той же схеме: S=π*a*b.
Но чаще можно столкнуться с полукруглыми или «полуовальными» помещениями. Для подсчёта размеров такой комнаты к формулам для круга и овала в конце дописываем /2. На латыни это будет выглядеть так: S=πr2/2 и S=π*a*b/2.
Многоуровневый пол
Встречается ещё реже. И посчитать его площадь можно так, как и в примере с прилегающими помещениями — сложить показатели каждого фрагмента. Но, если вам нужно такой пол покрасить, то не забудьте учесть и вертикальные плоскости. В противном случае краски на них может не хватить.
В конце хотелось бы отметить, что главное в любых расчётах — точность. Поэтому будьте внимательны при выполнении замеров и тщательно проверяйте результаты вычислений. Это значительно упростит дальнейшие, более сложные действия во время ремонта.
- 5
- 4
- 3
- 2
- 1
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны. Определение ромба звучит точно также, поэтому мы их объединили и расскажем про общие формулы расчета площади фигуры.
1. S = a * h, где a — сторона, h — высота.
2. S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето — прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.
 Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».
Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».
Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела, а σ — площадь поперечного сечения провода в физике. Это основные символы, хотя могут быть и другие, например, в сфере сопротивления материалов, А — площадь сечения профиля.
Советы и рекомендации
Таким образом можно рассчитать площадь всей квартиры и покрасить ее в разные цвета. Добавлены размеры всех стен и потолков — мы получаем число, которому следует руководствоваться при покупке стройматериалов.
Все, что вам нужно сделать, это пойти в магазин и купить припасы. Тут еще посчитать придется, ведь не все пакеты рассчитаны на большие помещения. Например, размер потолка на кухне 3х3. Сколько квадратных метров штукатурки нужно, если одним пакетом можно покрыть 3 квадратных метра? Допустим, площадь потолка 9 квадратных метров. Одной упаковки хватит на 3 кв. Поэтому нам понадобится 3 пакета на весь потолок.
Если на упаковке указано, что расход составляет 12 м2, это означает, сколько продукта необходимо для стены размером 3 x 4 м2.
Или другой пример. Стена в квартире 6 х 4. Сколько квадратных метров нужно покрасить? Умножьте 6 на 4, и вы получите 24 квадратных метра. Сколько нужно 3-литровых банок с краской, если каждая из них умещается на 6 квадратных метров? Давайте посчитаем 24, разделив на 6. Это 4. Итак, чтобы покрыть всю стену, вам нужно купить 4 трехлитровых банки с краской.
Всегда лучше брать с собой запасные части для ремонта, чтобы потом не приходилось возвращаться в магазин. В дальнейшем, когда нужно что-то покрасить или побелить, могут пригодиться остатки материалов.
С чего начинать
Перед проведением измерений следует подготовить:
- место;
- инструменты.
Комнату нужно освободить от разных предметов, которые в ней находятся. Если убрать все предметы из помещения не возможно, по крайней мере освободите стены, чтобы можно было беспрепятственно измерять. Замеры осуществляются рулеткой, поэтому стены помещения должны быть открыты для манипуляций.
Для замеров потребуются инструменты:
- рулетка: механическая, более точная электронная (лазерная);
- инструмент для определения ровности линии. К примеру, строительный уровень, большой угольник или циркуль;
- карандаш, лист бумаги;
- калькулятор;
- малярный скотч (узкий) для вспомогательной разметки на полу.
Проверьте, насколько четкая геометрия у комнаты, прямоугольная ли она. Это можно сделать путем замеров диагоналей. Длину стены замеряют по плинтусу.
Опытные профессионалы пользуются специальными лазерными линейками, которые позволяют точно снять замеры и произвести все нужные расчеты.
При манипуляции лента для замеров должна быть натянута
Обращайте внимание на то, по какой линейке вы проводите измерение – сантиметровой или дюймовой, чтобы не спутать метрические системы
Каждый параметр следует замерять минимум трижды и выводить среднее арифметическое. Работы проще проводит с помощником, это упростит процесс и сделает его более быстрым и в то же время точным.
Перед тем, как вычислить площадь комнаты, набросайте простейшую схему помещения, на которую потом нанесете полученные величины. При этом соблюдайте пропорции.