Конус

Как сделать елку из конуса своими руками

Прекрасное дополнение новогоднего праздника – елка, сделанная своими руками. Для этого необходимо сделать картонный конус любым из приведенных выше способов. Главное, чтобы он был прочным и правильной формы. После стоит приступить к ее украшению.

Дальнейшие действия заключаются в следующем:

1. Конус полностью обклеивается скотчем. Для обмотки можно использовать пищевую пленку.
2. Выбираются самые толстые (можно разноцветные) нитки и обмакиваются в клее ПВА. Клей можно предварительно разбавить чистой водичкой из расчета 1:1.
3. Нитки наматываются вокруг конуса.
4. Изделие оставляется для полной просушки.
5. Аккуратно через дно вытаскивается бумажный конус с пленкой. Застывшие нитки в форме конуса остаются невредимыми.
6. Полученная елка может быть украшена по желанию бантиками, ленточными, бусинками, блестками, декоративными фруктами, сделанными самостоятельно елочными игрушками.

Образующая конуса

Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:

g = √(r2 + h2)

Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:

g = h/sin(φ);

g = r/cos(φ)

Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.

Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.

Схемы способов обработки конических поверхностей

Способы обработки конических поверхностей внутреннего характера заключаются в резцовом растачивании детали с использованием конусной линейки, а также оборачивании верхней части суппортов.

Внешние конусы обрабатывают:

• вращением суппортов;
• смещением точек задней бабки;
• широкими резцами;
• конусной линейкой.

Полости конусообразных изделий создаются путем зенкерования и развертки. Данные методики дают возможность получить отверстия диаметрами высокой точности. С целью формирования дыр в сплошном металле используют сверла малого диаметра для нанесения разметки. После чего применяют зенкер или сверлильную ступенчатую установку.

Вращение верхнего суппорта 1 под заданным углом способствует подаче ручного и механического резца. Этот процесс осуществляется на токарных станках классического и автоматизированного типа. Повороты суппортов имеют угол α корпусного наклона, цифровое значение которого можно увидеть на фланцевой шкале 2.

Конические изделия большой длины отделывают путем смещения корпуса задней бабки. В этой процедуре резец двигается диаметрально по вертящейся заготовке с применением механического воздействия.

При данном точении угол наклона α конического изделия совпадает с наклонением резцового инструмента. Требуемое цифровое значение уклона достигается путем перемещения заднего пункта в противоположное направление.

Способы обработки конических поверхностей широкими режущими инструментами токарного оснащения основаны на движении кромок вдоль и поперек диаметра детали.

Резцовая обработка помогает выпускать крупные партии мелких деталей не более 20 мм диаметром, надежно защищенных от вибрационной деформации. 

Конусные линейки дают возможность обтачивать детали с углом наклона меньше, чем 10-12 градусов. Линейки закрепляются на станковом оборудовании. Для поступательного скользящего движения ползуна на начале точения выкручивают винт и отводят верхний суппорт от каретки снизу.

Отделка конуса с использованием станковой линейки осуществляется в специальной последовательности, отраженной на рисунке.

Плитка 11 зафиксирована к корпусу станка, оснащена конусной линейкой 9. Последняя может быть повернута под требуемым кругом пальца 8 по оси отделываемой конической детали.

Болты 4 и 10 необходимы с целью крепежа линейки. Ползун, обозначенный 7, скользящим движением объединяется с нижней суппортной салазкой 12 благодаря наличию зажима 6 и механизму тяготения 5. Низ суппорта отделяют от кареты 3 путем выкручивания гайки или поперечного болта.

Движения ползуна обуславливают возможность резцовой обработки внешней и внутренней поверхности конусообразной детали с углом уклона, равным значению α поворотов линейки.

С целью определить правильность отделки поверхности конусной детали и исключения брака наносят меловые линии по длине образующей.

После на изделие надевают калибр и поворачивают на половину оборота. Если нанесенные линии стерлись прерывчато, конусное изделие возвращают на исправление.

История создания

Появления такой конструкции, а так же происхождение самого названия до сих пор покрыто множеством тайн. Достоверно известно, что в 1863 году американский инженер Стивен Морзе зарегистрировал патент на изобретение спирального сверла, такого, которое известно нам и по сей день. До этого для изготовления сверла, скручивали заостренный плоский профиль.

В описании, запатентованного Стивеном Морзе спирально м сверле, нет никаких упоминаний об особой форме хвостовика, но по какой-то причине Бюро стандартов США внесло коническую форму в национальные стандарты. Считается, что изобретатель, запатентовав новую конструкцию сверла, направил опытные образцы в Бюро патентов, где была замечена и по достоинству оценена эта особенность.

Впоследствии была создана компания по производству, получившая его имя и занимавшаяся изготовлением инструмента для машиностроения. К концу 19 века компания серьезно расширилась и стала одним из ведущих производителей инструмента того времени. Произведенный ей продукт поставлялся во многие страны мира, в том числе и в Россию. За время ее существования было запатентовано еще несколько изобретений, но, ни одно из них не было связано с коническим исполнением хвостовиков инструмента. Так же есть сведения, что через какое-то время после основания сам изобретатель по неизвестным причинам покинул компанию, при этом его имя в названии сохранилось.

Так же известно еще несколько изобретателей с фамилией Морзе, живших в США в то время. И, возможно, автором этого изобретения является кто-то из них, но никакой информации, подтверждающей эту версию, нет. Поэтому официальным изобретателем конической формы хвостовика инструмента считается именно Стивен Эмброуз Морзе.

https://youtube.com/watch?v=evWPoMxRr-Q

Усеченный конус. Усiчений конус

Часть конуса, заключенная между его основанием и некоторой плоскостью, которая параллельная основанию и пересекает конус, называется усеченным конусом.

Частина конуса, укладена між його основою і деякою площиною, яка паралельна основи і перетинає конус називається усіченим конусом.

D1 – верхнее основание; D – нижнее основание. Высотой усеченного конуса называется расстояние между плоскостями оснований. Усеченный конус, который является частью прямого конуса, можно получить вращением прямоугольной трапеции OO1D1D вокруг ее высоты OO1. По аналогии с цилиндром и призмами вводятся понятия описанной около конуса и вписанной в конус пирамиды.

D1 — верхня основа; D — нижня основа. Висотою конуса називається відстань між площинами основ. Усічений конус, який є частиною прямого конуса, можна отримати обертанням прямокутної трапеції OO1D1D навколо її висоти OO1. За аналогією з циліндром і призмами вводяться поняття описаної близько конуса і вписаною в конус піраміди.

ПОИСК

На чертеже пиноли 2 (рис. 16.6) подчеркнуты сопряженные размеры диаметры 30 20 и 17, 780 мм, конусность 1 20, 020 (конус Морзе № 2). Размер 18 глубины расточки диаметром 30 мм равен размеру длины гайки 4 (см. рис. 16.8). Длина 150 мм определена из цепочки размеров длины винта со стороны трапецеидальной резьбы и длины конуса Морзе центра, расположенного в пиноли.

При упоре винта в торец центра между торцом буртика винта и торцом гайки (и пиноли) должен оставаться зазор 2…3 мм для осевого перемещения винта при выталкивании центра. Цепочка размеров винта и центра (размерная цепь) равна 94+(85—23—4)=152 мм, где 94 — длина части винта (см. рис. 16.12)  [c.

332] Конус Морзе Общие размеры Конструкции I и II Конструкция I/  

Каждую переходную конусную втулку обозначают номерами конуса Морзе. Основные размеры переходных втулок для инструмента с конусом Морзе установлены ГОСТом 9288-59.

Короткие переходные втулки (тип 1) выпускают со следующими номерами конусов Морзе 2-1, 3-1, 3-2, 4-2, 4-3, 5-3, 5-4, 6-4 и 6-5 (первая цифра характеризует  

Фрезы диаметром 20 мм исполнения 1 по соглашению с потребителем изготовляются с конусом Морзе 2. Размеры конусов Морзе по ГОСТ 2847-67,  

Конусы Морзе укороченные — Размеры 540  

Диаметр резьбы, в мм М конуса Морзе Наибольший размер патрона, в мм  

Размеры хвостовиков у сверл № конуса Морзе патрона Размеры патрона, в мм  

Конус Морзе № Размеры (в мм)  

Конусности общего назначения нормальные — Угол конуса — Примеры применения 129, 130 Конусы Морзе — Размеры 131 Координаты установки угловых фрез — Формулы для определения 465  

Конусы Морзе( ) Резьбы трубные конические общего назначения а также обсадных свыше бурильных и насосно-компрессорных труб. Конусы инструментов по американскому стандарту размерами 2-12″  

Применение углов конусов и конусностей специального назначения (табл. 22) регламентировано и допускается а предусмотренных случаях к числу их относятся инструментальные конусы Морзе, конические трубные резьбы, концы шпинделей металлорежущих станков, присоединительные размеры патронов и планшайб и др.  

Под конусы Морзе и метрические конусы широко применяют комплекты разверток из трех штук. Третья — чистовая развертка (фиг. 52) такая же, как в комплекте из двух разверток. Первая развертка (фиг. 54) — черновая, вторая развертка (фиг. 55) — промежуточная. Размеры разверток комплекта из трех штук приведены в табл. 78—79.  

Для чего используется конус

Мы подробно разобрали самые простые варианты как сделать правильный конус из бумаги. Для чего используется эта поделка? Направления у нее самые различные:

• геометрических выставок;
• объемных поделок;
• изготовления маскарадных шляп.

Ваша фантазия подскажет вам, где еще может применяться конус. А мы поможем вам вдохновиться с помощью простой конусной поделки елочки.

Ёлка из конуса

Для нее потребуется:

• картон;
• бумага для подарков;
• скотч;
• декоративные предметы;
• ножницы.

В основе изделия, как вы уже поняли, лежит конус. Изготовьте его по одной из предложенных выше инструкций.

Далее работаем по схеме:

1. Полученный конус, оборачиваем бумагой для подарков. Крепим кончик материала к верхушке скотчем и аккуратно оборачиваем бумагу по фигуре. Отрезаем лишний материал.
2. Крепим концы с помощью скотча.
3. Вы не поверите, но елочка готова. Осталось ее украсить как настоящую. С этой целью могут подойти пуговицы, большие бусины и миниатюрные новогодние игрушки.

В ёлке можно сделать отверстия. И если она достаточно широка, поместите внутрь конуса новогодние огоньки. В темноте, они будут приятно мелькать, создавая приятную атмосферу.

Как сделать конус из круга

Сделать конус из бумаги достаточно просто. Нужно только все делать правильно и аккуратно, предвещая уникальный положительный результат. Поэтапная инструкция заключается в следующем:

1. Определяется, для чего вы изготавливаете бумажный конус. От этого будут зависеть его размеры, плотность бумаги, цветовая гамма, а также наличие всяких декоративных элементов.
2. Берем бумагу нужного размера и раскладываем ее на горизонтальной поверхности. Для этого подойдет кухонный стол, тумбочка или журнальный столик. Как кому удобно.
3. Используя линейку, отмечается точка в середине листа.
4. В эту точку выставляется острие циркуля и предварительно очерчивается контуры круга пунктиром. При этом отмечается, не заходит ли грифель за пределы листа бумаги. Если все в порядке, проводится четкая линия.
5. Четко по линии ножницами вырезается круг.
6. Далее надо соединить линейкой центр круга с любой точкой окружности и провести линию карандашом.
7. При помощи ножниц аккуратно разрезать круг по этой линии точно до центра.
8. Разрезанный круг сворачивается в конус до такого размера, который вам необходим. Края подравниваются и закрепляются посредством скрепки.
9. На края разрезанных кромок с внутренней и внешней стороны наносится клей, и стенки плотно фиксируются.
10. Приступаем к изготовлению основания конуса. Для этого берется еще один лист бумаги и выкладывается на столе.
11. Изготовленный конус кладется на линейку. Так определяется его диаметр. От этого результата отнимается 2 миллиметра и показатель делится пополам. Это предполагаемый радиус конуса.
12. На чистом листе установленного радиуса прочерчивается карандашом круг. Он считается внутренним.
13. Затем из того же центра вычерчиваем новый круг, диаметр которого на 2-3 сантиметра превышает предыдущий.
14. Вырезаем круг по внешнему контуру.
15. Промежуток между внутренним и наружным кругом соединяем насечками, которые делаются с использованием ножниц. Желательно эту процедуру делать аккуратно, чтобы не выйти за пределы внутренней окружности. Расстояние между насечками должно составлять около сантиметра.
16. Изготовленные насечки заворачиваются в одну сторону. Должен получиться небольшой нахлест.
17. Внешнюю часть насечек покрываем клеем и аккуратно вставляем внутрь самого конуса.
18. Готовое изделие оставляем на столе и даем возможность ему тщательно высохнуть.

Основание конуса

Чтобы узнать радиус основания конусного каркаса, линейкой производят измерение диаметра нижней части заготовки, представляющую собой бумажную (картонную) боковую поверхность.

1. Для большей точности линейку прикладывают к краям заготовки и измеряют расстояние в двух перпендикулярных направлениях. Вычисляют среднее значение диаметра и делят пополам. В итоге получают величину радиуса основания бумажного конуса.
2. Циркулем на приготовленном втором листе бумаги чертят окружность, радиус которой равен половине диаметра основания конуса. На этом этапе изготовления нужно примерить основание уже сделанной боковой поверхности к нарисованному кругу. И, если всё совпадает, тогда приступают к следующему шагу.
3. Поставив ножку циркуля в центр начерченного круга, увеличивают раздвижение циркуля, делая припуск в 1,5 сантиметра, и рисуют ещё одну окружность.
4. По черте внешней окружности вырезается ножницами круг и делаются надрезы по всему периметру от края вырезанного круга до линии внутренней окружности.
5. Насечки загибают в одну сторону под углом 90 градусов. Получается дно конуса с загнутыми краями для соединения с боковой поверхностью.
6. Остаётся промазать клеем нижнюю внутреннюю часть боковины клеем на глубину 1,5 см и аккуратно вставить изготовленное дно насечками внутрь конуса.

Поэтапно построить готовую развёртку любого размера для конусного изделия можно и с помощью компьютера в графическом редакторе. После прорисовки чертежа в компьютерной программе его нужно распечатать на принтере, а потом останется только ножницами отделить лишнее и склеить готовую фигуру. Такой вариант особенно удобен, если нужно сделать игрушку в виде усечённого конуса.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

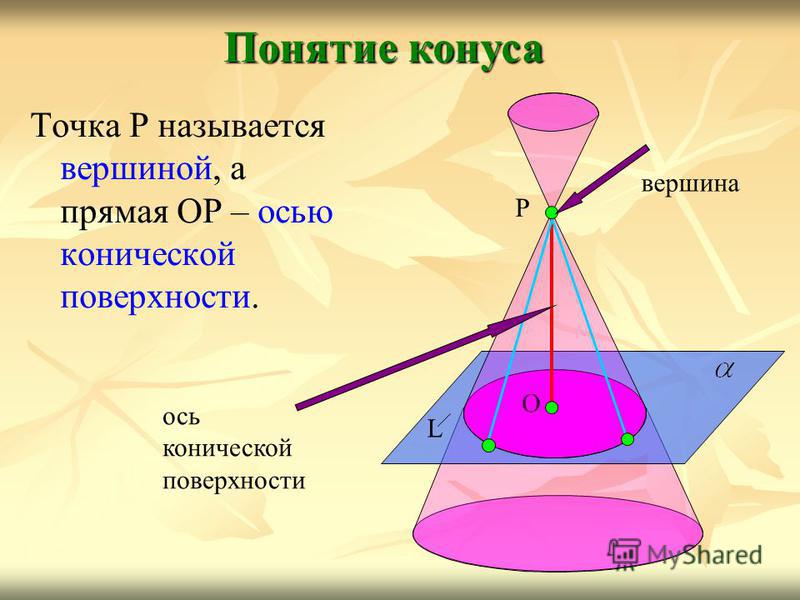
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

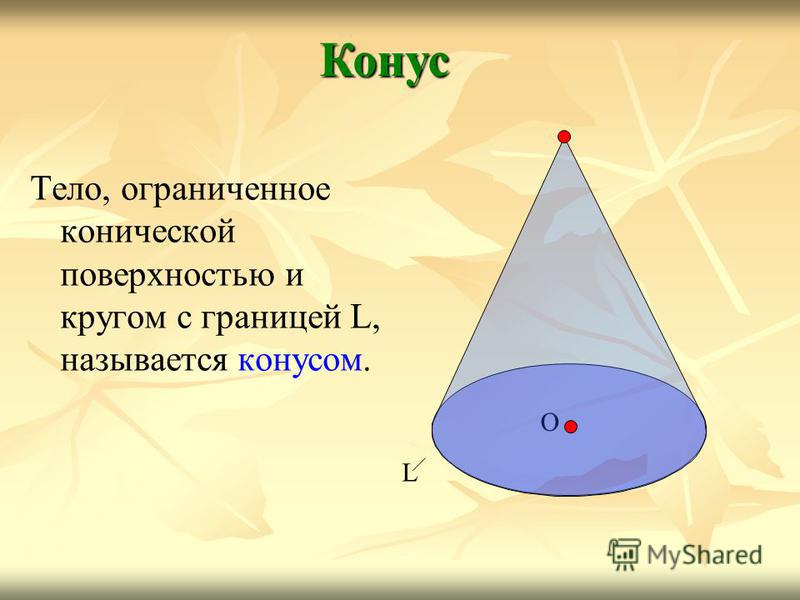
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

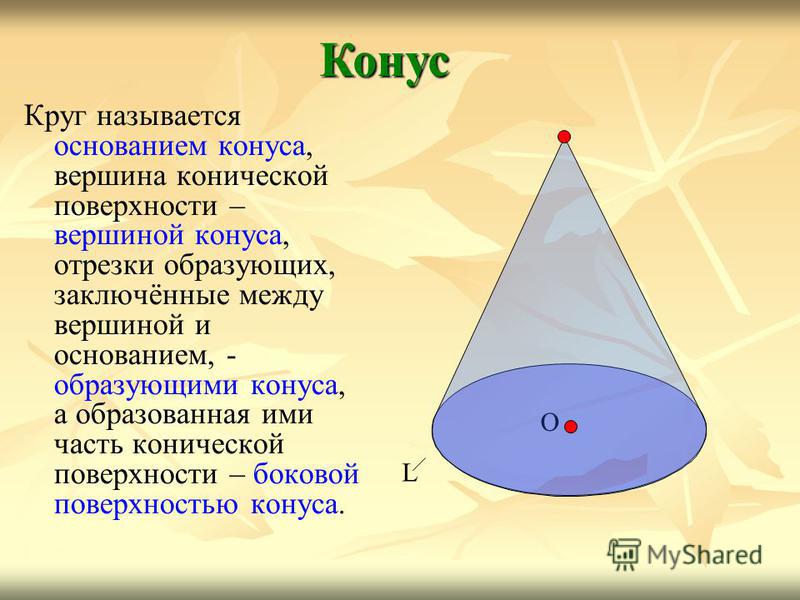
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

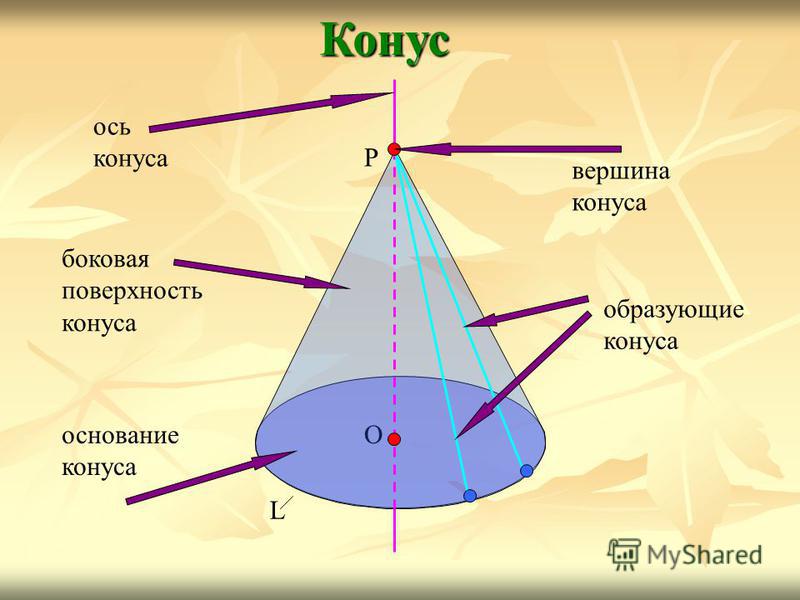
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

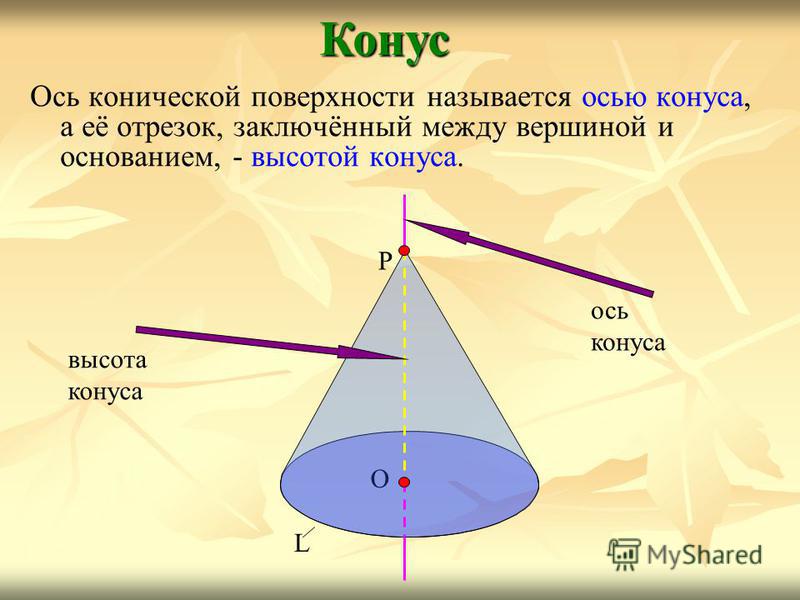
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

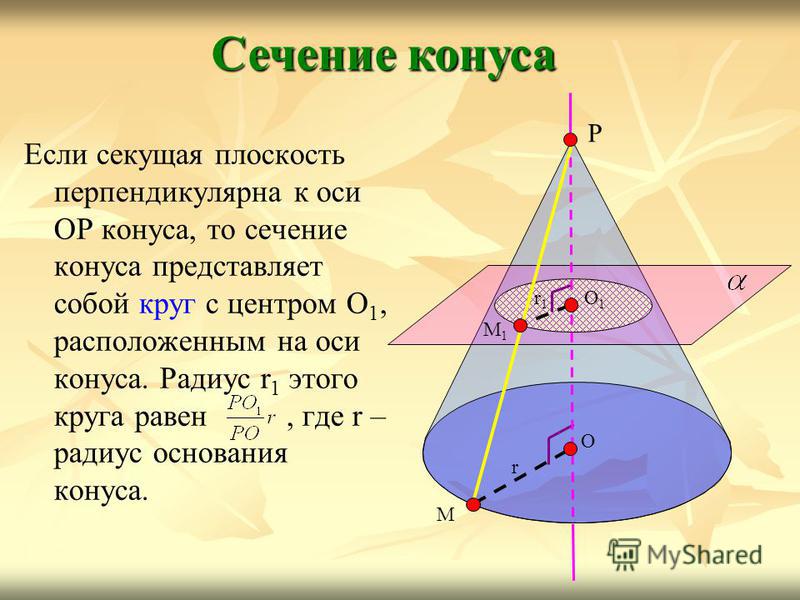
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

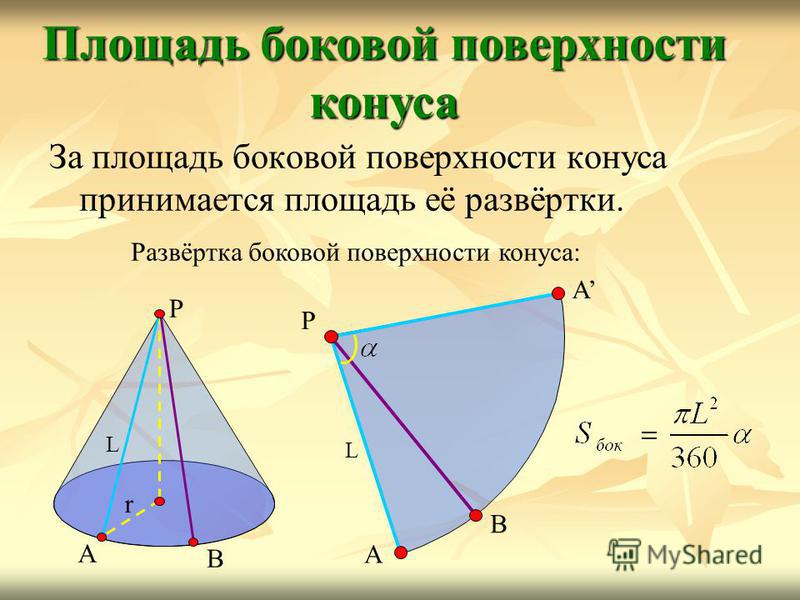
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

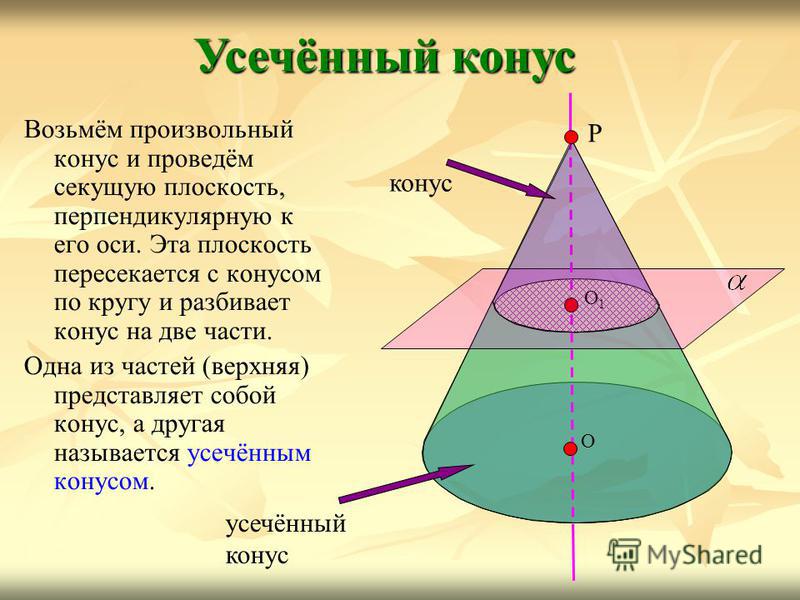
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

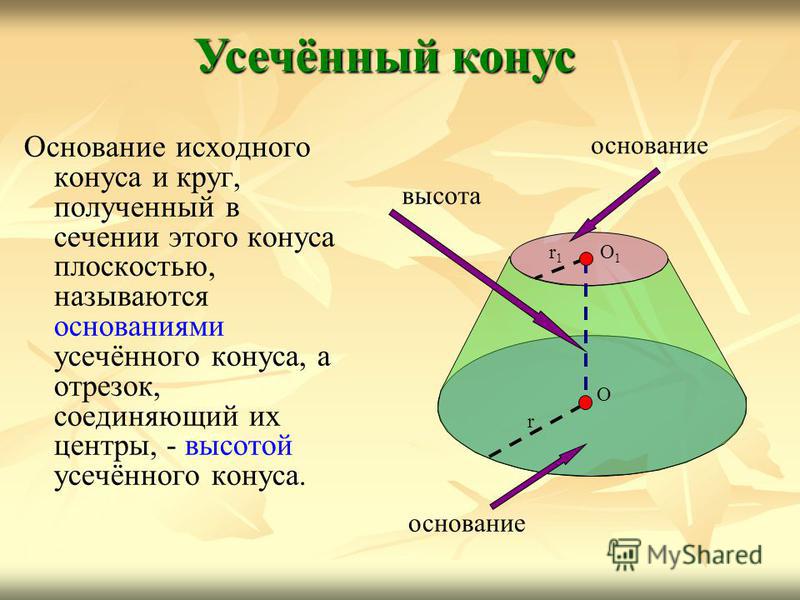
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

17

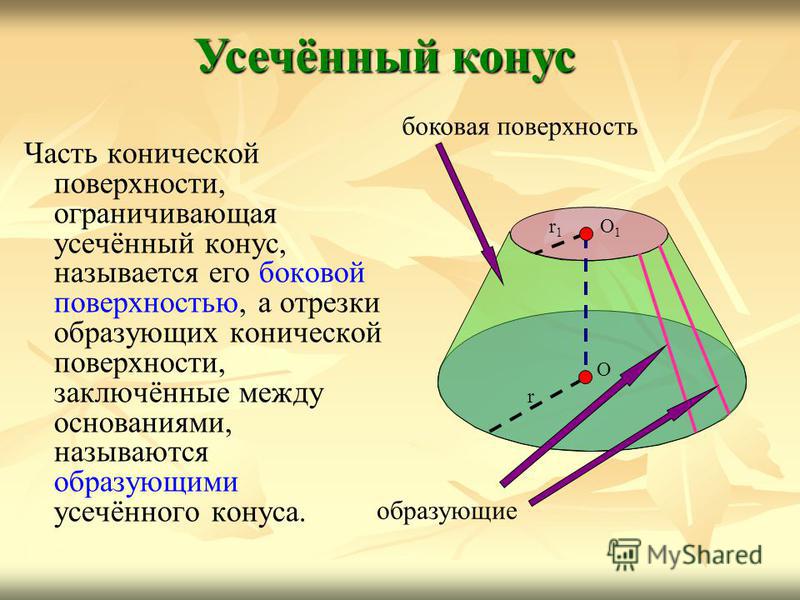
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

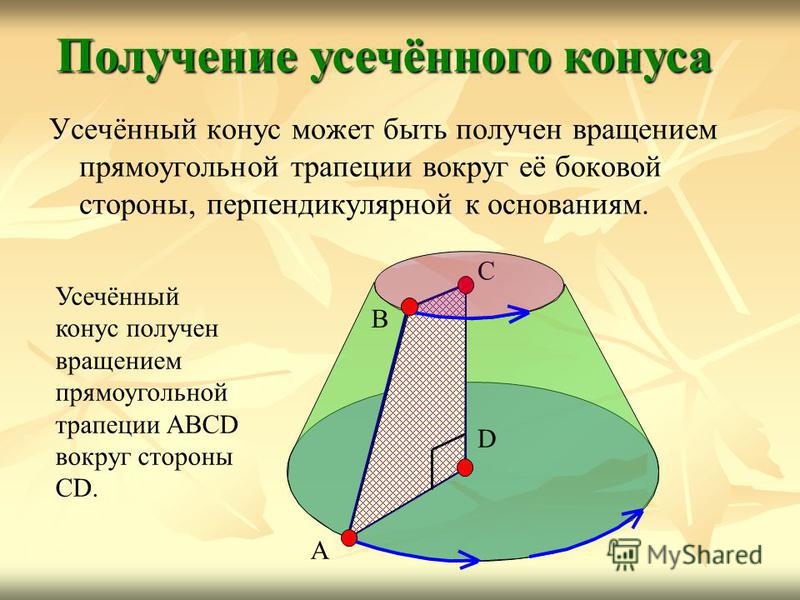
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

19

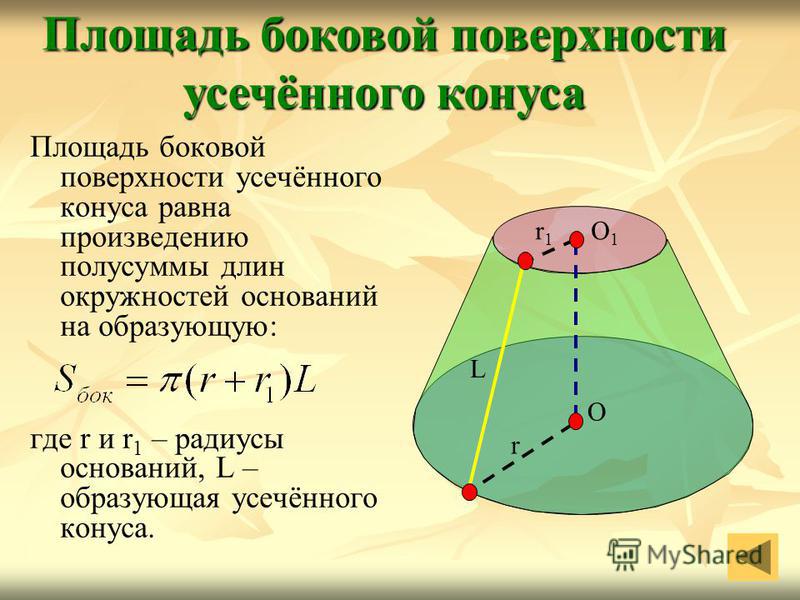
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

Развертка (выкройка) конуса

• Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
• Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
• Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
• Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
• Следующий калькулятор интересен тем, что он переводит древние российские денежные…
• Следующий калькулятор будет очень полезен тем, кто решил купить или…
• Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
• Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
• Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
• Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
• Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
• Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
• Следующий необычный калькулятор переводит меры длины из русской системы в…
• Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
• Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
• Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
• Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
• Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
• Как вы уже могли заметить на нашем сайте есть несколько…
• Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
• Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
• Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
• Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
• Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
• Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
• Перед вами отличный помощник для IT специалистов. С помощью данного…
• Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
• Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
• Начнем с истории. В 17 веке итальянским ученым Торричелли было…
• Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…

hostciti.net

Определение конуса и его элементов. Визначення конуса та його елементів

Рассмотрим в плоскости ограниченную фигуру D и точку S пространства, не лежащую в данной плоскости. Объединение всех отрезков SM, где M ∈ D, называется конусом с вершиной в точке S и основанием D.

Розглянемо в площині обмежену фігуру D і точку S простору, яка не лежить у цій площині. Об’єднання всіх відрізків SM, де M ∈ D, називається конусом з вершиною в точці S і підставою D.

Отрезок перпендикуляра, проведенного через вершину конуса к плоскости основания, называется высотой конуса. Боковой поверхностью конуса является коническая поверхность, у которой вершина находится в точке S, а направляющей является граница фигуры D. Если основанием конуса является круг, и вершина конуса проецируется в центр круга, то такой конус называется прямым круговым конусом.

Відрізок перпендикуляра, проведеного через вершину конуса до площини основи, називається висотою конуса. Бічною поверхнею конуса є конічна поверхня, вершина якої знаходиться в точці S, а направляючої є межа фігури D. Якщо основою конуса є круг, і вершина конуса проектується в центр кола, то такий конус називається прямим круговим конусом.

Наглядное представление о конусе можно получить вращением прямоугольного треугольника вокруг одного из его катетов. Тогда гипотенуза описывает боковую поверхность, а катет, не лежащий на оси вращения – основание конуса.

Наочне уявлення про конусі можна отримати обертанням прямокутного трикутника навколо одного з катетів. Тоді гіпотенуза описує бічну поверхню, а катет, не лежить на осі обертання — основа конуса.