Построение уклона и конусности

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Конус Морзе и метрический конус

Конус Морзе № 2 (MT2).

Схема инструментального конуса (наружные конусы с лапкой, наружные конусы без лапки, внутренние конусы (гнёзда)).

Конус Морзе — одно из самых широко применяемых креплений инструмента. Был предложен Стивеном А. Морзе приблизительно в 1864 году.

Конус Морзе подразделяется на восемь размеров, от КМ0 до КМ7 (англ. Morse taper, MT0-MT7, нем. Morsekegel, MK0-MK7). Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26″ до 3°00’52″, уклон конуса от 1°25’43″ до 1°30’26″) в зависимости от типоразмера.

Стандарты на конус Морзе: ISO 296, DIN 228, ГОСТ 25557-2016 «Конусы инструментальные. Основные размеры.». В российском стандарте конус КМ7 отсутствует, вместо него применяется несовместимый метрический конус № 80. Конусы, изготовленные по дюймовым и метрическим стандартам, взаимозаменяемы во всём, кроме резьбы хвостовика.

Существует несколько исполнений хвостовика конуса: с лапкой, с резьбой и без них. Инструмент с лапкой крепится в шпинделе заклиниванием этой лапки, для чего в рукаве некоторых шпинделей есть соответствующий паз. Лапка предназначена для облегчения выбивания конуса из шпинделя и предотвращения проворачивания. Инструмент с внутренней резьбой фиксируется в шпинделях штоком (штревелем), вворачивающимся в торец конуса. Конусы с резьбой гарантируют невыпадение инструмента и облегчают извлечение заклинившего конуса из шпинделя. Шпиндель обычно делается под один из вариантов фиксации — с лапкой, со штревелем или с фиксацией трением. Поскольку угол конуса меньше чем угол трения, фиксация хвостовика в гнезде может также происходить только за счет сил трения, без использования штревелей и лапок.

Некоторые конусы снабжаются системой отверстий и канавок для подачи смазочно-охлаждающей жидкости (СОЖ).

Метрический конус

По мере развития станкостроения понадобилось расширить диапазон размеров конусов Морзе как в большую, так и в меньшую стороны. При этом, для новых типоразмеров конуса, выбрали конусность ровно 1:20 (угол конуса 2°51’51″, уклон конуса 1°25’56″) и назвали их метрическими конусами (англ. Metric Taper). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2016 также определяет уменьшенные метрические конуса № 4 и № 6 (англ. ME4, ME6) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80 — ME200).

Конструктивных различий между конусом Морзе и метрическим нет.

Таблица 1

Обозначение конуса Конусность D D₁ d d₁ d₂ d_{3 max} d_{4 max} d₅ l_{1 max} l_{2 max} l_{3 max} l_{4 max} l_{5 min} l₆ Метрический № 4 1:20 4 4,1 2,9 – – – 2,5 3 23 25 – – 25 21

№ 6 1:20 6 6,2 4,4 – – – 4 4,6 32 35 – – 34 29

Морзе КМ 0 1:19,212 9,045 9,2 6,4 – 6,1 6 6 6,7 50 53 56,3 59,5 52 49

КМ 1 1:20,047 12,065 12,2 9,4 M6 9 8,7 9 9,7 53,5 57 62 65,5 56 52

КМ 2 1:20,020 17,780 18 14,6 M10 14 13,5 14 14,9 64 69 75 80 67 62

КМ 3 1:19,992 23,825 24,1 19,8 M12 19,1 18,5 19 20,2 80,1 86 94 99 84 78

КМ 4 1:19,254 31,267 31,6 25,9 M16 25,2 25,2 24 26,5 102,5 109 117,5 124 107 98

КМ 5 1:19,002 44,399 44,7 37,6 M20 36,5 35,7 35,7 38,2 129,5 136 149,5 156 135 125

КМ 6 1:19,180 63,348 63,8 53,9 M24 52,4 51 51 54,6 182 190 210 218 188 177

КМ 7 1:19,231 83,058

–

285.75

294.1

Метрический № 80 1:20 80 80,4 70,2 M30 69 67 67 71,5 196 204 220 228 202 186

№ 100 1:20 100 100,5 88,4 M36 87 85 85 90 232 242 260 270 240 220

№ 120 1:20 120 120,6 106,6 M36 105 102 102 108,5 268 280 300 312 276 254

№ 160 1:20 160 160,8 143 M48 141 138 138 145,5 340 356 380 396 350 321

№ 200 1:20 200 201 179,4 M48 177 174 174 182,5 412 432 460 480 424 388

1. В ГОСТ 25557 абберевиатура КМ отсутствует, типоразмер обозначен только цифрой
2. Отсутствует в ГОСТ 25557

Укороченные конуса Морзе

Для многих применений длина конуса Морзе оказалась избыточной. Поэтому были придуманы девять типоразмеров укороченных конусов Морзе, полученных «удалением» примерно половины исходных конусов. Цифра в обозначении укороченного конуса — округлённый диаметр новой толстой части конуса в мм. Российский стандарт на укороченные конуса ГОСТ 9953-82 «Конусы инструментов укороченные. Основные размеры.». В скобках приведены обозначения по старому ГОСТ 9953-67 (с буквой a конуса, у которых осталась более тонкая часть, а с буквой b — более толстая).

• B7 (0a) — укороченный до 14 мм КМ0.
• B10 (1a), B12 (1b) — укороченный до 18 и 22 мм соответственно КМ1.
• B16 (2a), B18 (2b) — укороченный до 24 и 32 мм соответственно КМ2.
• B22 (3a), B24 (3b) — укороченный до 45 и 55 мм соответственно КМ3.
• B32 (4b) — укороченный до 57 мм КМ4.
• B45 (5b) — укороченный до 71 мм КМ5.

Обозначение уклона в строительстве

Угол уклона — показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 «Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений«).

В соответствии с ГОСТ Р 21.1101-2013 «Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации», на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.

На разрезах, сечениях и схемах перед размерным числом, определяющим числовое значение уклона, наносят знак,

острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.

Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).

В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.

В промилле обозначают углы уклонов плоскостных сооружений — спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения — автомобильные и железные дороги.

Процент ( % ) — одна сотая доля. Промилле ( ‰ ) — одна тысячная доля.

Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра будет равен 5 % (читается как — пять сотых) или 50 ‰ (читается как — пятьдесят тысячных), это значение также будет соответствовать приблизительно — 3 о .

Часто спрашивают, что означает уклон, на пример 0,05 — это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 — см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.

Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.

Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.

Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка — 1:20 (4 / 0,2 = 20).

Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо — 0,2 м / (5 % / 100) = 4 м.

Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо — 5 % / 100 х 4 м = 0,2 м.

Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.

Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.

Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число — 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице — 0,0524, будет соответствовать углу 3 о (см. таблицу).

Источник

Конус Морзе и метрический конус

Конус Морзе — одно из самых широко применяемых креплений инструмента. Был предложен Стивеном А. Морзе приблизительно в 1864 году .

Конус Морзе подразделяется на восемь размеров, от КМ0

доКМ7 (англ. MT0-MT7 , нем. MK0-MK7 ) . Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26″ до 3°00’52″, уклон конуса от 1°25’43″ до 1°30’26″) в зависимости от типоразмера.

Метрический конус

По мере развития станкостроения понадобилось расширить диапазон размеров конусов Морзе как в большую, так и в меньшую стороны. При этом, для новых типоразмеров конуса, выбрали конусность ровно 1:20 (угол конуса 2°51’51″, уклон конуса 1°25’56″) и назвали их метрическими конусами

(англ. Metric Taper ). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2006 также определяет уменьшенные метрические конуса № 4 и № 6 (англ. ME4, ME6 ) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80 — ME200 ).

Конструктивных различий между конусом Морзе и метрическим нет.

Размеры наружного и внутреннего конуса (по ГОСТ 25557-2006), мм

Таблица 1

Обозначение конуса	Конусность	D	D 1	d	d 1	d 2	d 3 max	d 4 max	d 5	l 1 max	l 2 max	l 3 max	l 4 max	l 5 min	l 6
Метрический	№ 4	1:20	4	4,1	2,9	—	—	—	2,5	3	23	25	—	—	25	21
№ 6	1:20	6	6,2	4,4	—	—	—	4	4,6	32	35	—	—	34	29
Морзе	КМ0	1:19,212	9,045	9,2	6,4	—	6,1	6	6	6,7	50	53	56,3	59,5	52	49
КМ1	1:20,047	12,065	12,2	9,4	M6	9	8,7	9	9,7	53,5	57	62	65,5	56	52
КМ2	1:20,020	17,780	18	14,6	M10	14	13,5	14	14,9	64	69	75	80	67	62
КМ3	1:19,922	23,825	24,1	19,8	M12	19,1	18,5	19	20,2	80,1	86	94	99	84	78
КМ4	1:19,254	31,267	31,6	25,9	M16	25,2	25,2	24	26,5	102,5	109	117,5	124	107	98
КМ5	1:19,002	44,399	44,7	37,6	M20	36,5	35,7	35,7	38,2	129,5	136	149,5	156	135	125
КМ6	1:19,180	63,348	63,8	53,9	M24	52,4	51	51	54,6	182	190	210	218	188	177
КМ7	1:19,231	83,058	—	285.75	294.1
Метрический	№ 80	1:20	80	80,4	70,2	M30	69	67	67	71,5	196	204	220	228	202	186
№ 100	1:20	100	100,5	88,4	M36	87	85	85	90	232	242	260	270	240	220
№ 120	1:20	120	120,6	106,6	M36	105	102	102	108,5	268	280	300	312	276	254
№ 160	1:20	160	160,8	143	M48	141	138	138	145,5	340	356	380	396	350	321
№ 200	1:20	200	201	179,4	M48	177	174	174	182,5	412	432	460	480	424	388

Значение конусности

Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

1. Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
2. Для расчета примеряется следующая формула: i=AC/AB=tga.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.

Как подобрать угол уклона — несколько возможных вариантов

Гост 30893.2-2002. основные нормы взаимозаменяемости. общие допуски. допуски формы и расположения поверхностей, не указанные индивидуально

Существует несколько позиций, которыми руководствуются домашние мастера:

1. Сделать угол как можно более острым;
2. Сделать уклон минимальным или вообще пропустить этот пункт при монтаже канализационных стоков;
3. Создавать наклон согласно СНиПам, ГОСТам или специализированным справочникам.

На первый взгляд, излишне острый уклон канализационной трубы поможет воде, требующей очистки, быстрее доходить до пункта назначения. Но с другой стороны, при этом труба подвергается вредному воздействию стоков. Из-за того, что вода проходит по канализации слишком быстро, твердые частицы нечистот, пищевые остатки и прочий мусор, часто сливаемый в унитаз, остаются в трубе. Поэтому максимальный уклон трубы жестко регламентирован. Забегая вперед скажу, что он равен 15 см на 1 метр погонный.

Также проблемой станет заиливание трубы. Со временем канализация забьется и придется работать над её ремонтом. Срок службы такой системы значительно короче стандартного и составляет менее года.

Минимальный уклон или его отсутствие – это грубейшая ошибка при установке канализационного трубопровода. При этом труба не только заиливается, но и практически не очищается естественным путем.

Совет от эксперта: Правильнее всего работать с определенными нормативами, в которых указывается соотношение угла с диаметром и длиной трубы. Конечно, для этого требуется много времени и особая внимательность, но зато после такой кропотливой работы канализация прослужит Вам долгие годы.

Нормальные углы и конусности

Анализ конфигурации деталей машин и приборов показывает, что достаточно часто их поверхности располагаются под некоторым углом, отличным от прямого. В таком случае на расположение элементов деталей назначают угловые размеры с соответствующими допусками.

Угловые элементы деталей можно условно разделить на элементы с углами общего назначения и со специальными углами, размеры которых связаны расчетными зависимостями с другими принятыми линейными и угловыми размерами в силу специфических эксплуатационных или технологических требований.

С целью разумного ограничения номенклатуры углов первой группы, к которой относятся конструктивные наклонные поверхности с произвольными уклонами, скосы, фаски и др. ГОСТ 8908–81 устанавливает три ряда нормальных углов, причем каждый последующий ряд не поглощает предыдущие (таблица 23). В соответствии с принципом предпочтительности первый ряд имеет приоритет перед вторым, второй перед третьим.

Термины и определения, относящиеся к поверхностям и элементам деталей, имеющим угловые элементы, установлены ГОСТ 25548 – 82 .

Под прямой круговой конической поверхностью (конической поверхностью или конусом) понимают поверхность вращения, образованную прямой образующей, вращающейся относительно оси и пересекающей ее.

Ряды нормальных углов по ГОСТ 8908

Конус – обобщенный термин, под которым в зависимости от конкретных условий понимают коническую поверхность, коническую деталь или конический элемент детали.

В деталях конические поверхности часто стыкуются с цилиндрическими поверхностями на продолжении той же оси и имеют вид усеченного конуса с большим и меньшим основаниями.

Под основаниями конуса понимают круговые сечения, образованные пересечением конической поверхности с плоскостями перпендикулярными оси и ограничивающими его в осевом направлении.

Основной плоскостью называют плоскость поперечного сечения конуса, в котором задается номинальный диаметр конуса.

Базовой плоскостью является плоскость, перпендикулярная оси конуса и служащая для определения осевого положения основной плоскости или осевого положения данного конуса относительно сопрягаемого с ним конуса.Базовая плоскость может совпадать или не совпадатьс основной.

Элементы конусов обозначаются следующим образом (рис.3.92). Диаметры поперечных сечений конусов: большого основания – D; малого – d; заданного сечения (в котором задан допуск) – D_S, произвольно расположенного сечения – d_х. Угол конуса обозначают α, угол уклона конуса α/2. Параметры наружных конусов помечают индексом е, внутренних – i.

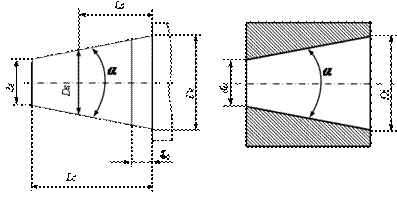
Рис. 3.92. Основные параметры конусов и конического соединения

Угол уклона конуса α/2 связан с размерами D, d и L следующим соотношением:

где С – конусность;

Приведенные взаимосвязи следует учитывать при назначении угловых и линейных размеров конусов и допусков этих размеров.

При необходимости различения параметров конических соединений, наружных и внутренних конусов в обозначениях параметров наружных конусов используют индексы e, параметров внутренних конусов индексы i, а для параметров конических соединений – р.

Обозначение длины конуса – L, длины конического соединения – L_р, осевое расстояние от большего основания конуса до заданного сечения – L_S, до произвольно расположенного сечения – L_х. Расстояние между основной и базовой плоскостями конуса (базорасстояние конуса) обозначают z_e или z_i, а базорасстояние конического соединения – z_p.

Усеченный конус (наружный и внутренний) характеризуется диаметром большого основания D, диаметром малого основания d, длиной конуса L и углом конуса α.

188.64.169.166 studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock! и обновите страницу (F5)очень нужно

Техническое черчение

Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:

i=AC/AB=tga

Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)

k=(D-d)/l=2tga

Таким образом,

k = 2i

Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.

Например: конусность, выраженная в градусах — 11°25’16»; отношением — 1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38»; отношением — 1:10; дробью—0,1; в процентах — 10%.

Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.

Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):

1) построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2) опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм. Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2. В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:

ps/np=10/100,

откуда

ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

i=ps/np=1/6

где i — заданный уклон.

Подставив в формулу числовые значения, получим

ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание!

Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно!

Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса

При этом важно, чтобы она была перпендикулярна осевому сечению

Конус Морзе

Для быстрого, точного и надежного центрированного способа крепления инструмента используется хвостовик в виде конуса и коническое отверстие для него в шпинделе фрезерного станка. Чаще всего в сверлах, фрезах, зенковках и другом режущем инструменте применяется конус Морзе.

Он бывает 8-ми размеров: от КМ нулевого размера до КМ седьмого размера. Этот вид хвостовика был изобретен Стивеном А. Морзе (он также первым придумал спиральное сверло).

Существует еще 9 размеров укороченных конусов Морзе: В45, В32, В24, В22, В18, В16, В12, В10 и В7 (приведены в порядке убывания).

Так, российским стандартом не рекомендовано использовать конус Морзе КМ7 – вместо него разработан метрический конус №80, который несовместим с КМ7.

В остальном конусы, производимые по международным (дюймовым) и российским (метрическим) стандартам, полностью взаимозаменяемы и отличаются лишь параметрами  резьбы хвостовика.

Хвостовик инструментального конуса исполняется в нескольких вариантах: с резьбой, с лапкой или без них. Внутренняя резьба, имеющаяся в торце конуса, служит для фиксации инструмента в шпинделе с помощью специального штока – штревеля.

Во-первых, она облегчает выбивание конуса из шпинделя, а во-вторых, не позволяет инструменту проворачиваться при больших нагрузках.

В некоторых конусах Морзе предусматривается целая система канавок и отверстий, через которые к режущим органам инструмента подается смазочно-охлаждающая жидкость (СОЖ).

А вот в станках с ЧПУ (в том числе и настольных) широко используется автоматическая смена инструмента. Для этих целей разработан специальный инструментальный конус, который устраняет такие недостатки конуса Морзе, как

• частое самозаклинивание хвостовика в шпинделе;
• большая длина хвостовика;
• небольшая площадь торца хвостовика и, как следствие, недостаточный осевой упор;
• множество сложностей, возникающих при автоматическом закреплении конуса инструмента в шпинделе;
• невозможность автоматической смены инструмента из-за отсутствия зацепов на хвостовике.

Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

История создания

Появления такой конструкции, а так же происхождение самого названия до сих пор покрыто множеством тайн. Достоверно известно, что в 1863 году американский инженер Стивен Морзе зарегистрировал патент на изобретение спирального сверла, такого, которое известно нам и по сей день. До этого для изготовления сверла, скручивали заостренный плоский профиль.

В описании, запатентованного Стивеном Морзе спирально м сверле, нет никаких упоминаний об особой форме хвостовика, но по какой-то причине Бюро стандартов США внесло коническую форму в национальные стандарты. Считается, что изобретатель, запатентовав новую конструкцию сверла, направил опытные образцы в Бюро патентов, где была замечена и по достоинству оценена эта особенность.

Впоследствии была создана компания по производству, получившая его имя и занимавшаяся изготовлением инструмента для машиностроения. К концу 19 века компания серьезно расширилась и стала одним из ведущих производителей инструмента того времени. Произведенный ей продукт поставлялся во многие страны мира, в том числе и в Россию. За время ее существования было запатентовано еще несколько изобретений, но, ни одно из них не было связано с коническим исполнением хвостовиков инструмента. Так же есть сведения, что через какое-то время после основания сам изобретатель по неизвестным причинам покинул компанию, при этом его имя в названии сохранилось.

Так же известно еще несколько изобретателей с фамилией Морзе, живших в США в то время. И, возможно, автором этого изобретения является кто-то из них, но никакой информации, подтверждающей эту версию, нет. Поэтому официальным изобретателем конической формы хвостовика инструмента считается именно Стивен Эмброуз Морзе.

Это интересно: Что такое канифоль и для чего она нужна — разбираем досконально